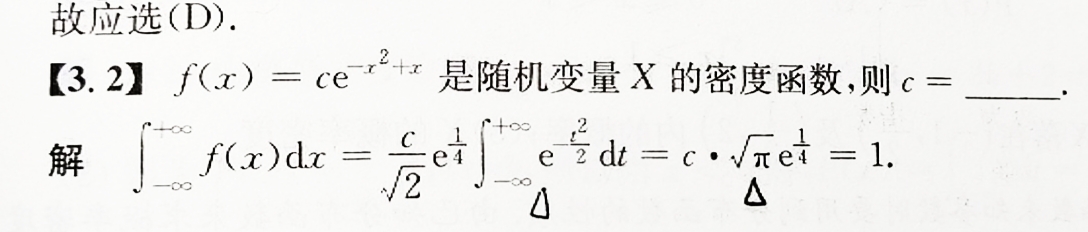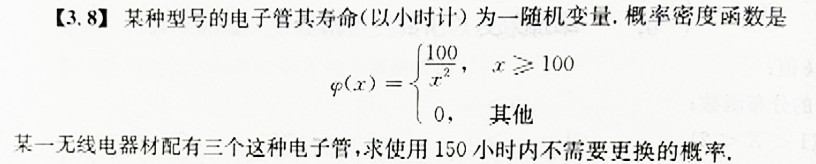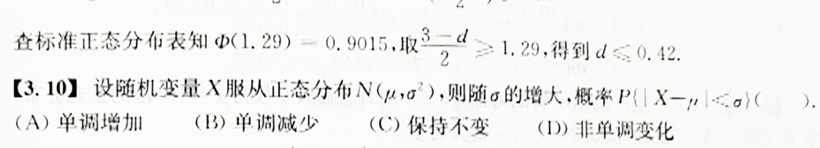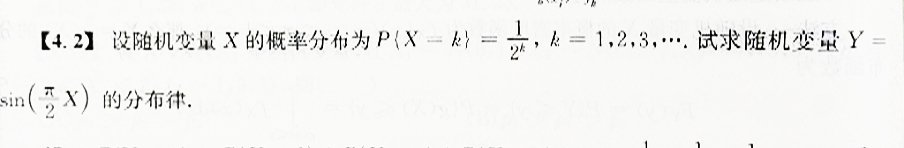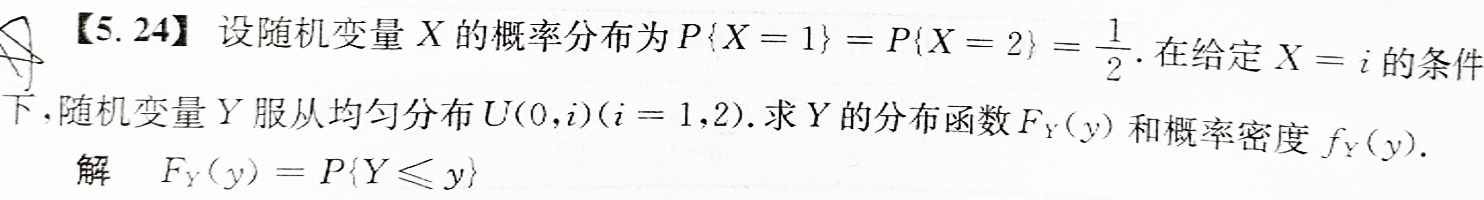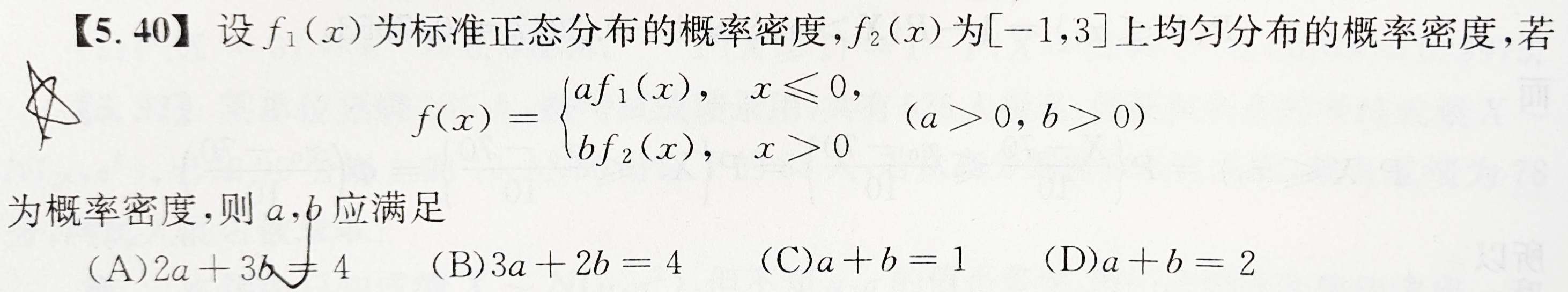当x<0时,F(x)=0.
当x≥2时,因为题目说射击都能中靶,所以F(x)=1.
当0<x<2时,F(x)=kπx2.
又∵分布函数是右连续的,∴x→2+limF(x)=4kπ=1
∴k=4π1F(x)=4x2.
综上,——

设需要配备N名工人,X为故障设备的台数,则X∼B(300,0.01),
故障但不能维修,即N<X.
∴P(X>N)≤0.01,∴P(x≤N)>0.99,
∵λ=np=3,由泊松定理知,P(X≤N)=k=0∑Ne−3k!3k,
∴P(X>N)=k=N+1∑∞e−3k!3k
然后,查表得当N≥8时上式成立。
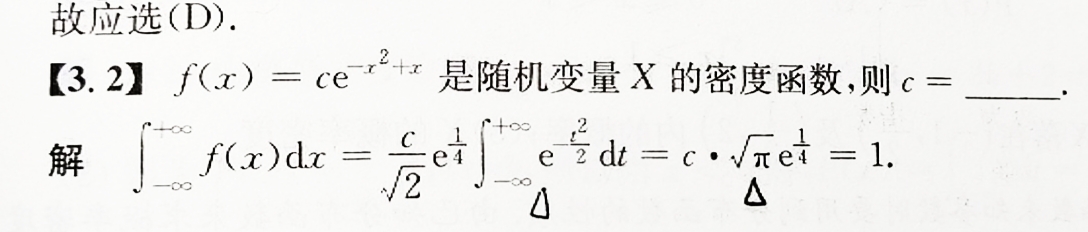
f(x)有两个性质,一个是f(x)>0,得到c>0(没有用)。
还有一个是积分等于1
先换元,令t=x−21,
∫−∞∞f(x)dx=ce41∫−∞∞e−t2dt
下面求解这个积分:∫−∞∞e−x2dx.这是一个超越积分,直接求不行,但他的平方可求。
(∫−∞∞e−x2dx)2
=∫−∞∞e−x2dx∫−∞∞e−y2dy
=∫−∞∞∫−∞∞e−(x2+y2)dxdy
=∫02π∫0∞e−r2rdrdθ
=21∫02πdθ=π
∴∫−∞∞e−x2dx=π,
∴原式=ce41π=1, ∴c=πe4.
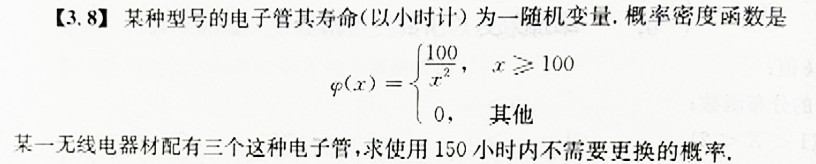
即这三个电子管寿命都大于150的概率。
P(X>150)=1−P(X≤150)=1−∫100150x2100dx=32
∴p=(32)3=278
(注意积分上下限,和理解题意)
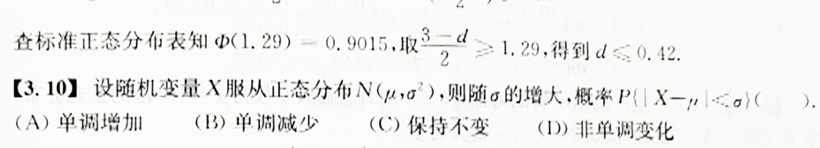
化为标准正态分布:
P(∣X−μ∣<σ)=P(∣Y∣<1)=Φ(1)−Φ(−1)
保持不变
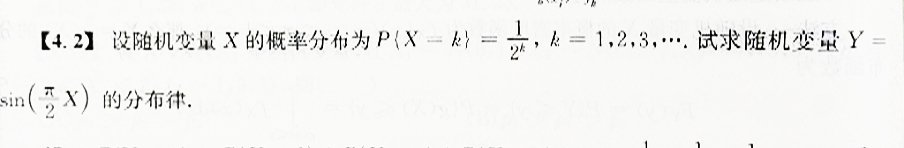
X的取值为1,2,3……,所以Y的取值为-1,0,1
∴P(Y=−1)=P(X=3)+P(X=7)+P(X=11)+⋯
=231+271+2111+⋯=152
P(Y=0)=P(X=2)+P(X=4)+P(X=6)+⋯
=221+241+261+⋯=31
P(Y=1)=1−P(Y=0)+P(Y=−1)=158
综上,…

这么精彩的推导,不好好看一看吗?
(1)当Y≤0时,f(y)=0
当Y>0时,
FY(y)=P(Y≤y)=P(eX≤y)=P(X≤lny)=Φ(lny)
∴fY(y)=FY′(y)=Φ′(lny)=2πy1e−2(lny)2
综上,分段…
(2)
当Y<1时,fY(y)=0,
当Y≥1时,
FY(y)=P(Y≤y)=P(2X2+1≤y)
=P(−2y−1≤X≤2y−1)=2π1∫−2y−12y−1e−2x2dx
∴fY(y)=FY′(y)=2π1e−4y−1(42y−11+42y−11)
=2π1e−4y−122y−11=2π(y−1)1e−4y−1
综上,分段…略
变上限函数的求导法则!!!
(3)与2同理,反而更简单

当X<−1时,F(X)=0,
当X>1时,F(X)=1,
当X=−1时,F(X)=81,
当−1<X<1时,
F(X)=P(X≤x)=P(X≤−1)+P(−1<X<x)=81+k(x+1)
∴F(1−0)=81+2k=1−41=43
∴k=165
∴F(X)=81+165(x+1)=165x+7
最后,分段综述
这题就是讲究严谨,画画图,理一下思路
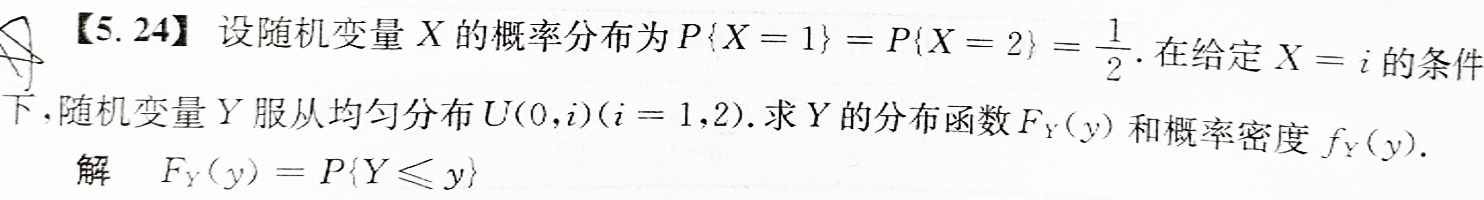
先全概率公式
=P(X=1)P(Y≤y∣X=1)+P(X=2)P(Y≤y∣X=2)
=21P(Y≤y∣X=1)+21P(Y≤y∣X=2)
当Y≤0时,FY(y)=0,fY(y)=0.
当Y>2时,FY(y)=1,fY(y)=0.
当0<Y≤1时,
FY(y)=21y+212y=43y
fY(y)=43
当1<Y≤2时,
FY(y)=0+212y=4y
fY(y)=41
综上,分段。。。
离散的和连续的混合起来了,第一眼看上去有点懵,如果想不到用全概率公式的话,还真没什么思路。

由题意得,1≤Y≤2,
∴当Y<1时,FY(y)=0.当Y>2时,FY(y)=1.
当1≤Y≤2时,
FY(y)=P(Y≤y)=P(Y=1)+P(1<Y<y)
=P(X≥2)+P(1<X<y)
=∫2391x2dx+∫1y91x2dx
=271(27−8+y3−1)=2718+y3
综上,。。。
不要陷入思维的误区,去考虑当X取什么值时FY的变化。要从Y的取值范围入手,进行分类讨论。

本题的难点是,利用90分和60分那两个数据,反求μ和σ.
同时,要有标准化的思想
∵P(X>90)=52612∴P(X≤90)=Φ(σ90−μ)=526514
反查表得:
σ90−μ=2
同理,利用P(X<60)可得
σ60−μ=1
即可联立解出μ=70,σ=10
然后,就简单了,布响写辣。

1−α=1−P(∣X∣<x)=P(∣X∣≥x)
=P(X≥x)+P(X≤−x)=2P(X≥x)
∴P(X≥x)=21−α∴x=u21−α
这谁会啊,woc
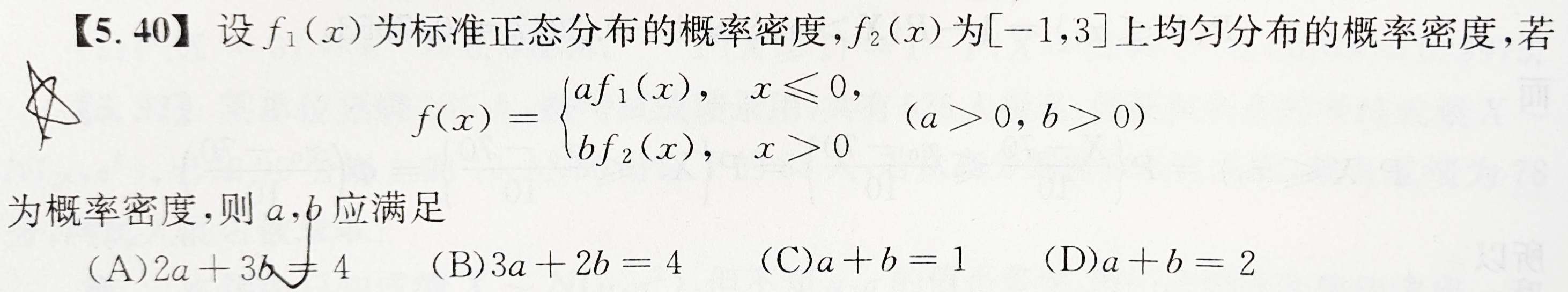
∵∫−∞∞f(x)dx=a∫−∞0f1(x)dx+b∫0∞f2(x)dx
且
∫−∞0f1(x)dx=21
∫0∞f2(x)dx=∫0341dx=43
∴2a+43b=1

快使用无记忆性大法!
P(Y≤a+1∣Y>a)=P(Y≤1)=1−e−1
乐

设X={蛋数},Y={鸡数},由全概率公式得
P(Y=n)=P(X=n)P(Y=n∣X=n)+P(X=n+1)P(Y=n∣X=n+1)+⋯
=n!λne−λpn+(n+1)!λn+1e−λCn+1npnq+⋯
=n!(λp)ne−λ(1−q)=n!(λp)ne−λp
所以,Y∼P(λp)