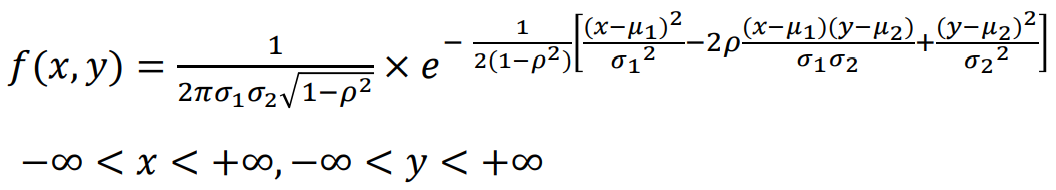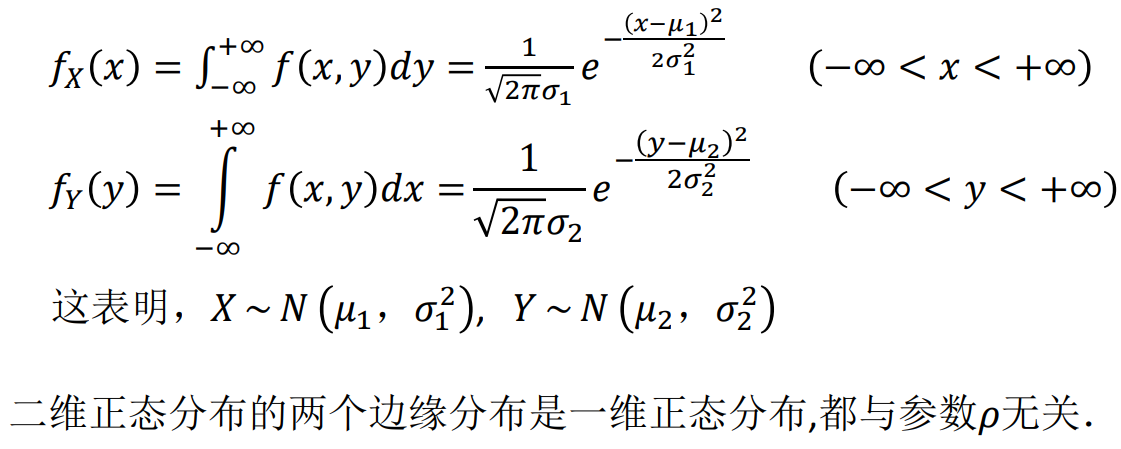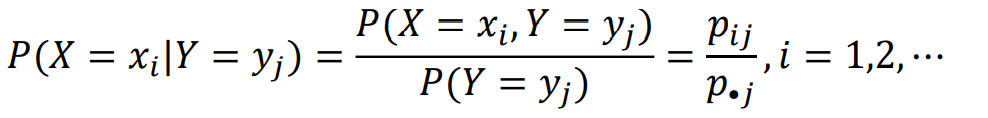二维随机变量及其分布
联合分布函数
定义
设 (𝑋, 𝑌) 为二维随机变量, 对任意实数 𝑥, 𝑦, 二元函数F(x,y)=P(X≤x,Y≤y)称为二维随机变量 (𝑋, 𝑌) 的联合分布函数, 简称为 (𝑋, 𝑌) 的分布函数.
性质
(1)0≤F(x,y)≤1,且F(+∞,+∞)=1,而F(−∞,+∞)=F(+∞,−∞)=F(−∞,−∞)=0.
(2)对每个变量单调不减
- 固定 x , 对任意的 y1<y2,F(x,y1)≤F(x,y2),
- 固定 y , 对任意的 x1<x2,F(x1,y)≤F(x2,y).
(3)对每个变量右连续
F(x0,y0)=F(x0+0,y0)=F(x0,y0+0).
离散型二维随机变量
联合概率分布如下,不必多说

0≤p(i,j)≤1,i,j=1,2,3⋯
i=1∑+∞j=1∑+∞p(i,j)=1
联合概率分布的计算
pij=P(X=xi,Y=yj)=P(X=xi)P(Y=yj∣X=xi)
F(x,y)=xi≤x∑yj≤y∑pij
P{(X,Y)∈G}=(xi,yj)∈G∑pij
连续型二维随机变量
定义
设二维随机变量(X ,Y )的分布函数为 F(x ,y), 若存在非负可积函 数 f (x,y) , 使得对于任意实数 x , y 有
F(x,y)=∫−∞x∫−∞yf(u,v)dudv
则称( X ,Y ) 为二维连续型随机变量,
f (x,y) 为( X ,Y ) 的联合概 率密度函数,简称概率密度函数,简记pdf (joint PDF)
性质
- f(x,y)≥0,在某些地方可以大于1
- F(+∞,+∞)=1
- ∂x∂y∂2F(x)=f(x,y).
- P{(X,Y)∈G}=G∬f(x,y)dxdy.
常用的二维连续型随机变量
均匀分布
 v
v
性质:
若G1⊆G,G1的面积为A1,那么P{(X,Y)∈G1}=GG1.
就是说,如果是均匀分布的话,概率为面积之比。
二维正态分布
若随机变量( X ,Y ) 的联合pdf为
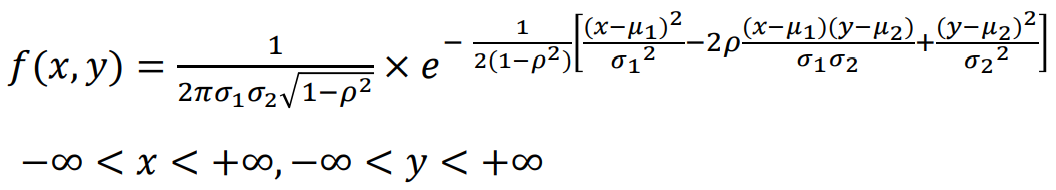
则称( X ,Y ) 服从参数为μ1,σ12,μ2,σ22,ρ的正态分布, 记作
(X,Y)∼N(μ1,σ12,μ2,σ22,ρ)
其中σ1,σ2>0,−1<ρ<1.
边缘分布
由联合分布函数可以得到边缘分布函数;反过来一般不成立.

离散型
即全概率公式

连续型
已知联合密度可求边缘密度
fX(x)=∫−∞+∞f(x,y)dy
同理,
fY(y)=∫−∞+∞f(x,y)dx
这里虽然说是从负无穷到正无穷积分,但是f(x,y)往往是分段的,实际操作时要进一步确定上下限。
关于正态分布:
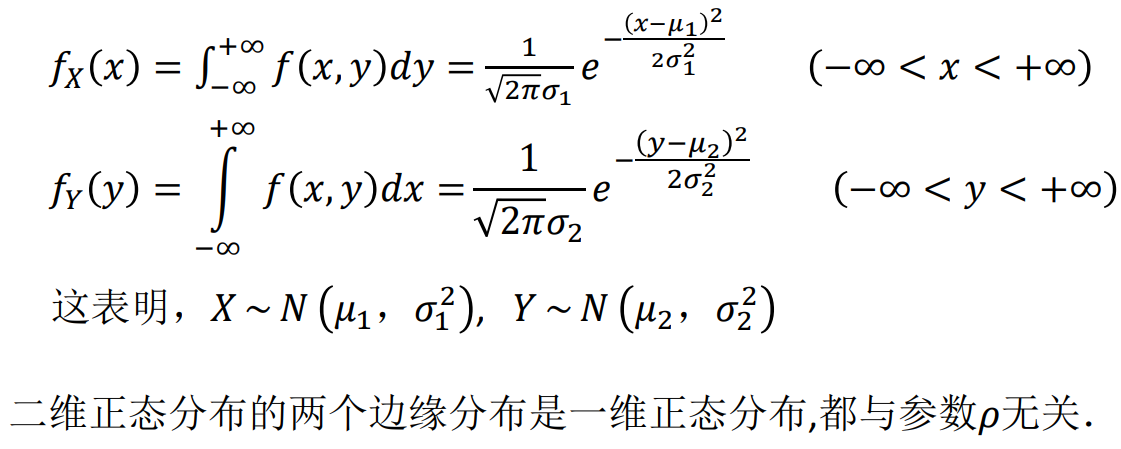
条件分布
离散型
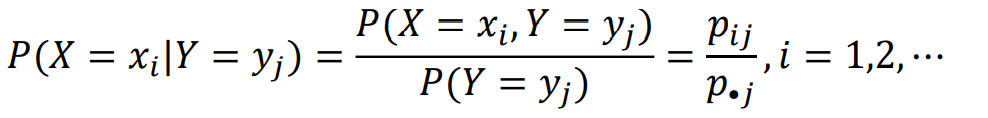
因为(X ,Y)是二维连续型随机变量时, P(X = x) = 0, P(Y = y) = 0 不能直接代入条件概率公式,所以利用极限的方法引入条件分布函数
连续型
因为当(X ,Y)是二维连续型随机变量时, P(X = x) = 0, P(Y = y) = 0 不能直接代入条件概率公式,所以

由此,可以得到在条件Y= y下X的条件分布函数
FX∣Y(x,y)=fY(y)∫−∞xf(u,y)du=∫−∞xfY(y)f(u,y)du
所以,
fX∣Y(x,y)=fY(y)f(x,y)
即联合密度除以边缘密度,
在实际操作的时候,同样要考虑分段的情况,尤其是当联合密度函数和边缘密度函数都分段且分段不同时,最终结果的分段区间需要仔细考虑。
省流

随机变量的独立性
定义
设X,Y是两个随机变量,若对任意的x,y,有F(x,y)=FX(x)FY(y),即P(X≤x,Y≤y)=P(X≤x)P(Y≤y),则称X,Y相互独立.
两个随机变量相互独立时,其联合分布函数等于两个边缘分布函数的乘积, 边缘分布完全确定联合分布.
性质
离散型
X与Y独立等价于对一切i,j有
- P(X=xi,Y=yj)=P(X=xi)P(Y=yj).
- pij=pi⋅p⋅j
连续型
X与Y独立等价于对任何x ,y 有
- f(x,y)=fX(x)fY(y)
- fX(x)=fX∣Y(x∣y),(fY(y)>0)
- fY(y)=fY∣X(y∣x),(fX(x)>0)
对于二维正态分布当X与Y独立时,等价于ρ=0.
拓展到n维随机变量
就是同理可得,
分布函数就是密度函数的n次重积分,边缘分布就是除所指定的维度之外的n-1次重积分
若F(x1,x2,…,xn)=FX1(x1)FX2(x2)…FXn(xn),则称随机变量X1,X2,…,Xn相互独立。
二维随机变量函数的分布
研究的是Z=g(X,Y)的概率分布,方法是把Z转化为(X,Y)的事件。
离散型
P(Z=zk)=P(g(X,Y)=zk)
=g(xi,yj)=zk∑P(X=xi,Y=yj)
注意,这里X,Y的取值范围是使得所有函数值等于z的x,y
连续型
总体思路
已知随机变量(X,Y)的密度函数求Z=g(X,Y)的密度函数的问题比较复杂,我们只讨论以下几种函数
- Z=X+Y
- Z=YX
- Z=max{X,Y}和Z=min{X,Y}
解决问题的方法是,先求分布函数,再求导得密度函数
(1)
FZ(z)=P(Z≤z)=P(g(X,Y)≤z)
=g(x,y)≤z∬f(x,y)dxdy
注意:积分域是随着z而变化的
(2)求导
fZ(z)=FZ′(z)
一般公式
如果Z=g(X,Y)中,(X,Y)到(Z,Y)或(Z,X)是一一对应变换的,有如下结论成立
设Y=h(X,Z)
fZ(z)=∫−∞∞f(x,h(x,z))∣∂z∂h∣dx
同理,设X=h(Z,Y)
fZ(z)=∫−∞∞f(h(z,y),y)∣∂z∂h∣dy
特别地,对于最大值,最小值函数
- 最大值函数:当g为max函数时,即要求X,Y的最大值小于等于z,只需要让X,Y都小于等于z即可
- 最小值函数:同理,取反面
所以,一览表
| g(X,Y) |
密度函数 |
| Z=X+Y |
∫−∞∞f(z−y,y)dy或∫−∞∞f(x,z−x)dx |
| Z=YX |
∫−∞∞f(yz,y)∣y∣dy |
| g |
max(X,Y) |
min(X,Y) |
| 二维 |
FX(z)FY(z) |
1−[1−FX(z)][1−FY(z)] |
| n维 |
FX1(z)FX2(z)…FXn(z) |
1−[1−FX1(z)][1−FX2(z)]…[1−FXn(z)] |
| 独立同分布(iid) |
[F(z)]n |
1−[1−F(z)]n |


 v
v