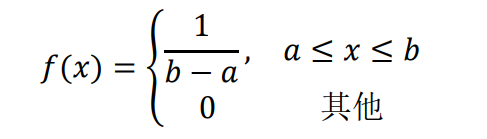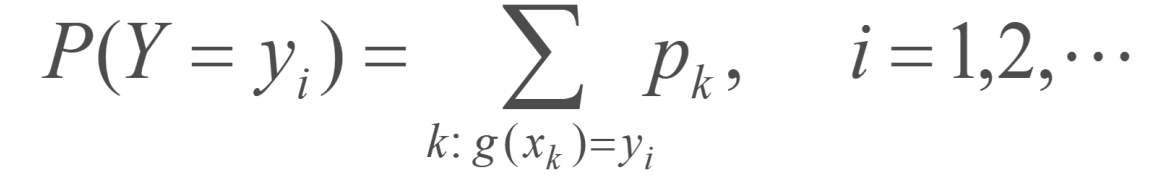一维连续型随机变量及其分布
cdf与pdf
定义
设F( x)是随机变量X的概率分布函数(cumulative distribution function, cdf),若存在非负可积函数f ( x)≥0,对任意实数x,有F(x)=P(X≤x)=∫−∞xf(t)dt−∞<x<+∞.
称X为连续型随机变量,f ( x)为X的概率密度函数 (Probability Density Function,pdf ).
性质
- f(x)>0,且在部分点处有可能f(x)>1.
- F(+∞)=1.
- P(a<x≤b)=F(b)−F(a)=∫abf(x)dx.
- 连续随机变量的cdf是连续函数,离散随机变量的cdf不一定连续.
- P(X=a)=0,a为任意指定值.
- P(A)=0⇒A=∅.
- P(B)=1⇒B=Ω.
Logistic distribution
作用:将在(−∞,+∞)上的变量映射到(0,1)上。
sigmoid函数:
F(x)=1+exex,x∈R
均匀分布
定义
如果连续型随机变量X具有密度函数
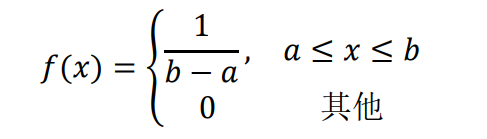
在指定区间内的所有值 都具有相同的概率,其中a, b是有限数,则称X是[a,b]上的均匀分布,记作 X~U [a,b].
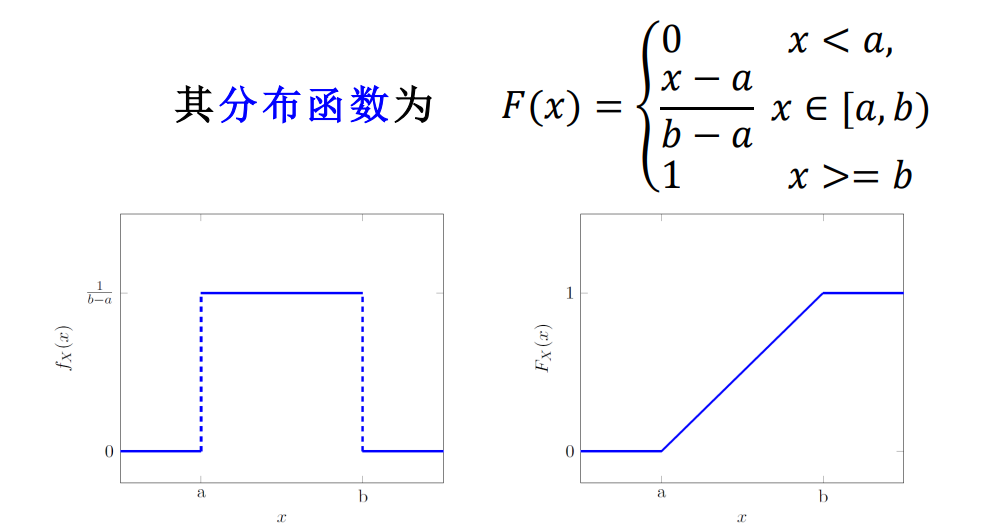
性质
均匀分布的特点:若X~U [a,b],则X 取值落在 [a,b]中的 某一区域内的概率与这一区域的长度成正比,而与区域的位 置无关.
均匀分布的重要性:借助于均匀分布可以生成任意的分布, 在计算机上很容易生成均匀分布.
Unif(0,1)经常称为标准分布(standard Uniform)
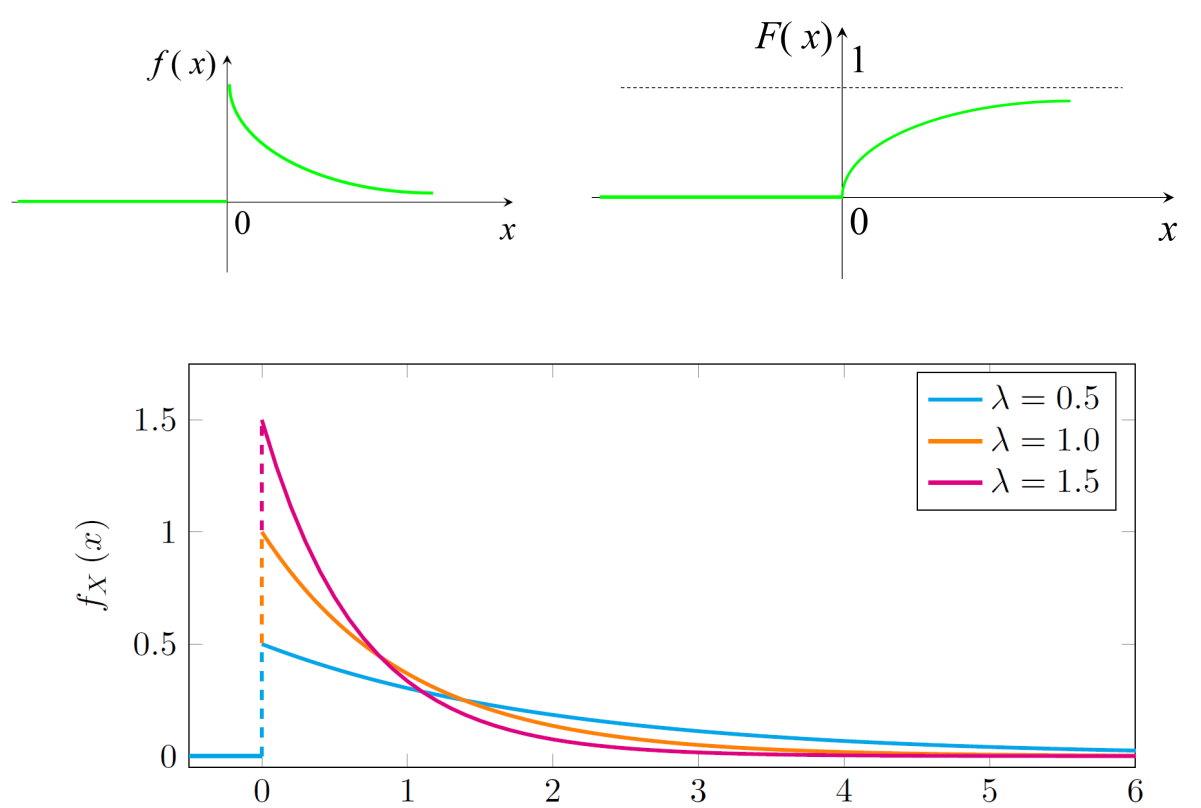
指数分布
定义
如果连续型随机变量X具有密度函数
f(x)={λe−λx,x>00,其他
这里λ>0为常数,则称X服从参数为λ的指数分布. 简记为X~E(λ). 其分布函数为
F(x)={0,x<01−e−λx,x≥0
指数分布常用来近似“寿命”问题,$\lambda $表示寿命的倒数。
指数分布的无记忆性
P(X>s+t∣X>s)=P(X>t)
理解:忽略了前s阶段的损耗.
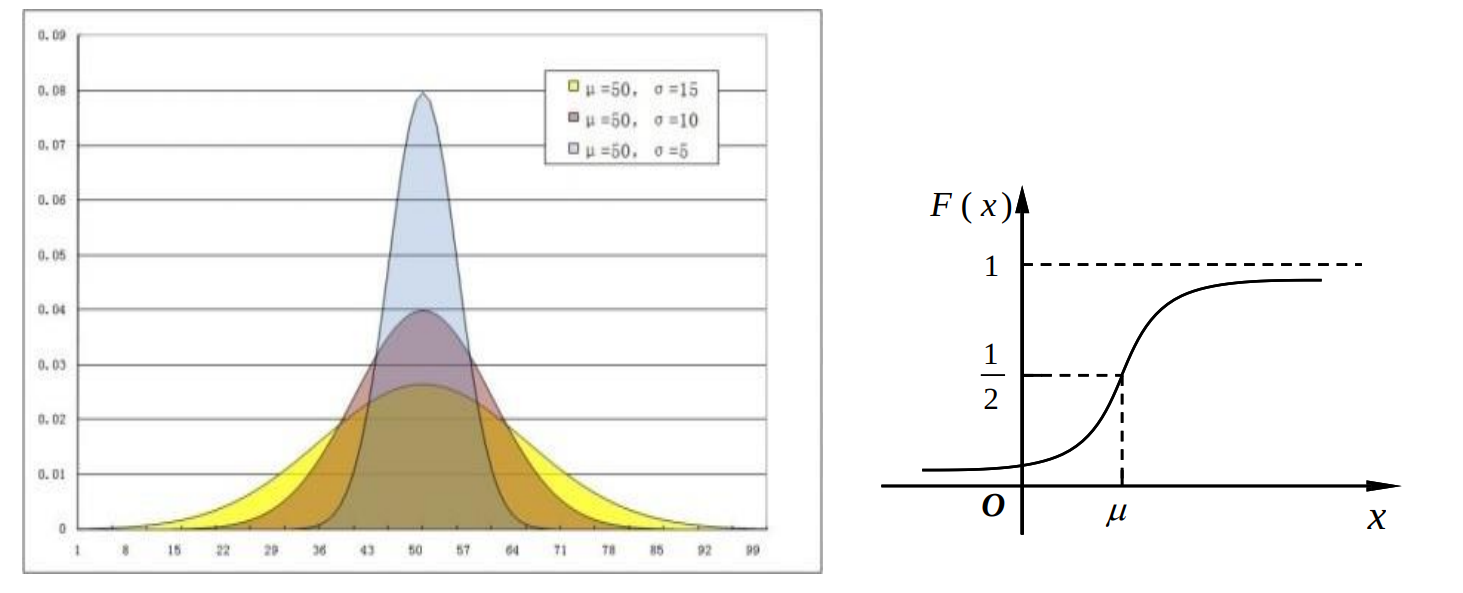
正态分布
定义
如果连续型随机变量X的密度函数
f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<+∞
其中μ,σ 为常数,且σ>0,则称随机变量X 服从参数μ,σ 的正态分布,记为X~N(μ,σ2).
分布函数没有解析表达式
小结论
对于标准的正态分布f(x)=2π1e−2x2,有如下结论成立
∫−∞∞f(x)dx=∫−∞∞x2f(x)dx=1
∫−∞∞xf(x)dx=∫−∞∞x3f(x)dx=0
∫−∞∞xd(f(x))=−∫−∞∞x2f(x)dx
∫0∞xf(x)dx=2π1
∫−∞∞∣x∣f(x)dx=π2
冷知识:在 x = μ±σ 时, 曲线 y = f (x) 在对应的点处有拐点
标准正态分布 X ~N (0,1)
- Φ(x)+Φ(−x)=1
- 通过Y=σX−μ,将一般正态分布转化为标准正态分布。
离散型随机变量函数的分布
我们已经知道了X的分布,还想知道Y=g(X)的分布,需要将与Y 有关的事件转化成 X 的事件。
注意合并:
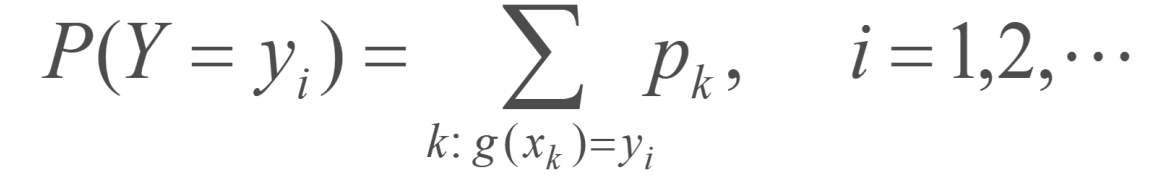
连续型随机变量函数的分布

方法二:

反变换定理
我去,这定理太邪门了

只要知道随机变量X服从的 分布函数cdf以及其cdf的反 函数,就可以通过计算机所 生成的[0,1]上的均匀分布生 成所需要的分布。
X=F−1(U)
F是已知的,U是计算机模拟的,所以就能产生X的分布
c++算法如下:
1
2
3
4
5
6
7
8
9
| double randomExponential(double lambda){
double pV = 0.0;
while(true){
pV = (double)rand()/(double)RAND_MAX;
if (pV != 1) break;
}
pV = (-1.0/lambda)*log(1-pV);
return pV;
}
|
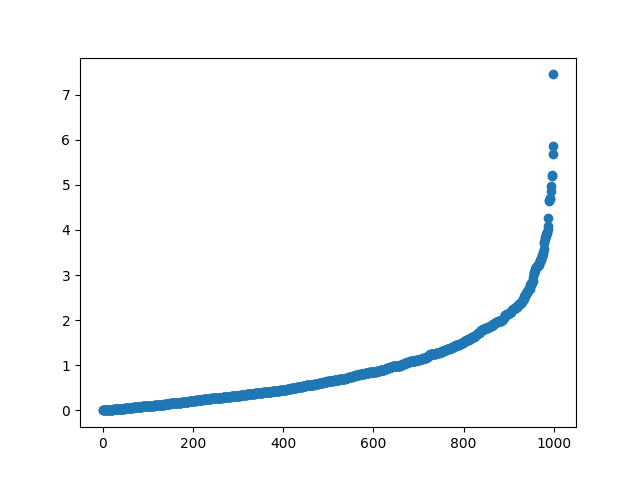
使用python实现λ=1时的指数分布:
1
2
3
4
5
6
7
8
9
10
11
12
13
| import numpy as np
import matplotlib.pyplot as plt
i = 0
y=[]
x=[]
while i<1000:
a=np.random.uniform()
y.append(-np.log(1-a))
x.append(i)
i=i+1
y.sort()
plt.scatter(x, y)
plt.show()
|
.