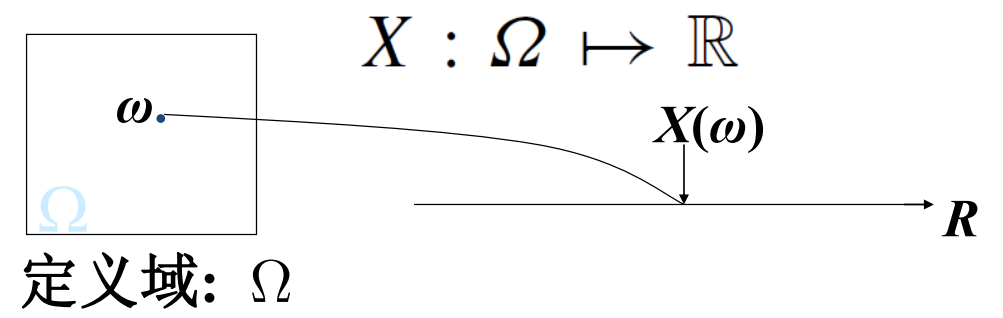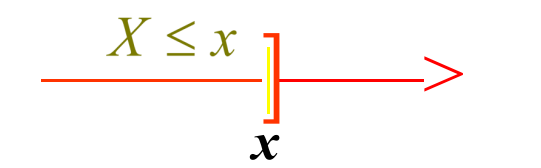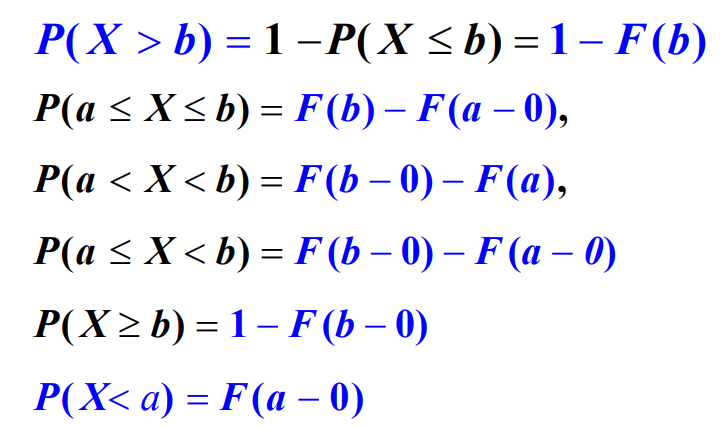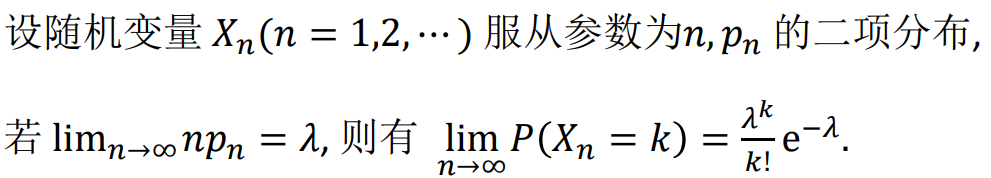概率论03

随机变量

设试验 E的样本空间为$\Omega$$，如果对于每一个样本点$$\omega\in\Omega$$，都有唯一实数$$X(\omega)$$与之对应，则称单值实函数 $$X=X(\omega)$$ 为样本空间$$\Omega$上的随机变量.

随机变量是一个函数，或者说它是一个因变量，它表示的是从样本空间到实数集合的一个映射。

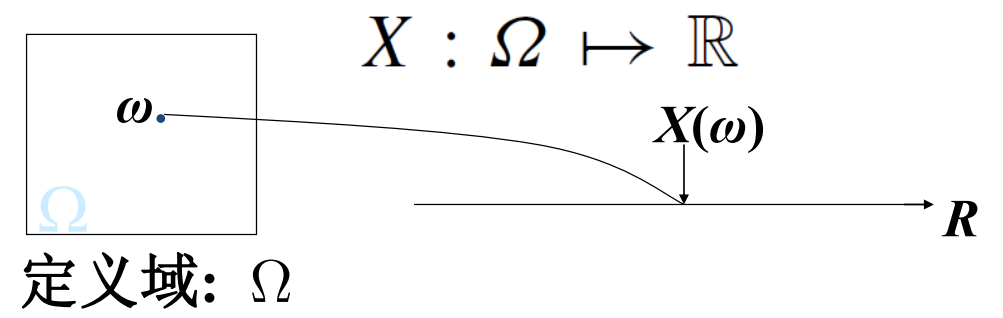
引入随机变量的意义：

1. 可以用随机变量来描述任何随机现象
2. 可以使用微积分了

累积分布函数（ cdf ）

定义

设X是定义在样本空间$\Omega$$上的随机变量，称函数 $$F ( x)= P{X\leq x}, −\infty< x <\infty$为随机变量X的概率分布函数也称累积分布函数。记为X~F(x).

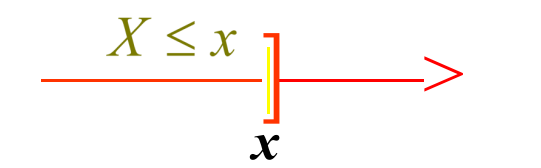
性质

（1）单调不减：$\forall a<b,F(a)\leq F(b)$,

（2）$0\leq F(x)\leq 1$:

$$\underset{x\rightarrow +\infty}{lim}F(x)=1,\underset{x\rightarrow -\infty}{lim}F(x)=0$$

（3）右连续：

$$\underset{x\rightarrow x_0^+}{lim}F(x)=F(x_0)$$

推论：

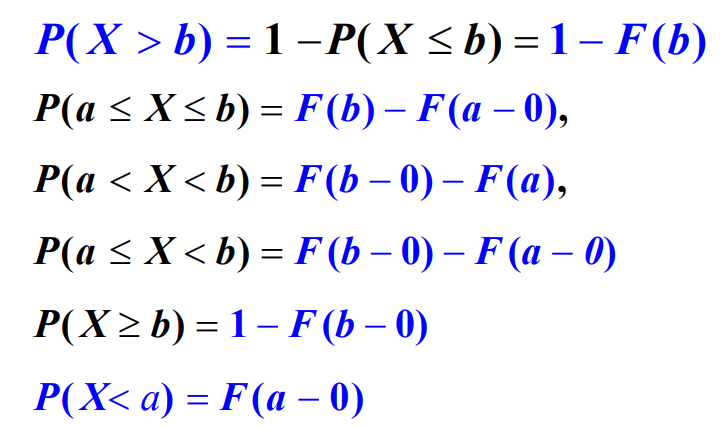
随机变量的分类

• 离散型

• 非离散型：连续型、其它类型

离散随机变量

设X是样本空间$\Omega$$上的随机变量．若集合$$\{X(\omega):\omega\in\Omega \}=\{x_1,x_2,...,x_n,... \}$是有限集或可列集，则称X是离散型随机变量．

概率分布函数(pmf)

$p_k=P(X=x_k),k=1,2,...$称为离散型随机变量X的概率分布或分布律(pmf)

性质

$p_k满足p_k\geq 0,k=1,2,...\underset{k}{\sum}p_k=1$.

用这些性质可以判断 是否为分布律

求离散随机变量的概率分布

(1)确定随机变量的所有可能取值; (2)计算每个取值点的概率.

$$P(X\in A)=\underset{x_n\in A}{\sum}p_n$$

cdf与pmf是等价的，对于离散型随机变量， pmf更直观与简便.

5种离散型随机变量的概率分布

两点分布(Bernoulli)

只有两种可能结果的随机现象， 随机变量X只可能取0与1两个值，则称X服从两点分布，记为X～Bern(p).

$P\{X = k\} = p^k (1−p)^{(1-k)}$ , 其中k = 0, 1.

几何分布(Geometric)

定义

在伯努利试验中，直到事件A第一次发生时所做的试验次数 X服从几何分布，即“第一次成功”分布。

若随机变量X 的分布列为:$0<p\leq 1,P\{X=k\}=(1-p)^{k-1}p,其中k=1,2,...$则称X服从几何分布,记为X～G( p).

它的含义是前k-1次实验都没有成功，第k次成功了；同理，“第2次成功”分布的含义是除了第k次成功了之外，前k-1次实验中还有一次成功了。

几何分布的无记忆性(Memoryless Property)

$$P(X = n + k | X>n) = P(X = k)$$

该性质表明，在前 n次试验中 A 没有出现的条件下，则在接下 去的 k次试验中 A仍未出现的概率只与 k有关，而与以前n次试 验无关，似乎忘记了前n次试验 结果，这就是无记忆性。

超几何分布(Hypergeometric)

$$P(x=k)=\frac{C_{N-M}^{n-k}C_M^k}{C_{N}^n}$$

$$k=0,1,...,min(M,n)$$

$min(M,n)$$就是说$$n\leq M$.

二项分布(Binomial)

定义

在n重贝努利试验中，事件A出现的次数记为X 服从二项分布。

记作X ~ B(n, p)，n指的是独立重复实验的次数，p指的是一次伯努利实验中A发生的概率。

pmf为：$P(X = k) = C_n^k p^k (1-p)^{n −k }, 0 \leq k \leq n$.

超几何分布与二项分布的关系

$$设N\rightarrow\infty时，\frac{M}{N}\rightarrow p$$

$$则\frac{C_{N-M}^{n-k}C_M^k}{C_{N}^n}=C_n^m p^m (1-p)^{n −m },(N\rightarrow\infty)$$

二项分布的最可能出现次数

(当x取多少时，概率最大)

泊松分布(Poisson)

定义

若随机变量X的分布列为$P\{X=\lambda \}=e^{-\lambda}\frac{\lambda^k}{k!}$$， $$k=0,1,2…$ $\lambda>0$$.则称X服从参数为$$\lambda$的泊松分布.

记为X～P($\lambda$).

泊松分布(稀有分布律)主要用于估计某稀有事件(rare events) 在特定时间内或空间中发生的次数.

泊松分布中最可能出现次数

• 当λ= 整数时,在λ与λ– 1 处的概率取得最大值

• 当λ$\not=$整数时, 在 [λ]处的概率取得最大值

二项分布的泊松近似

Possion定理：

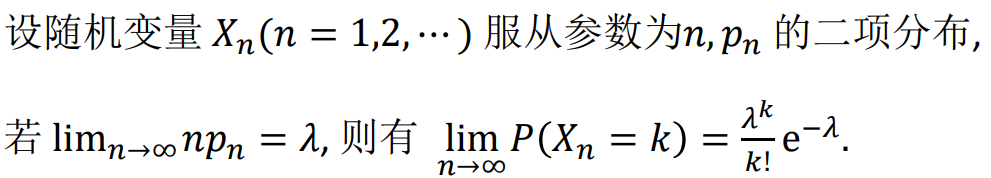
二项分布的极限分布是 Poisson 分布: