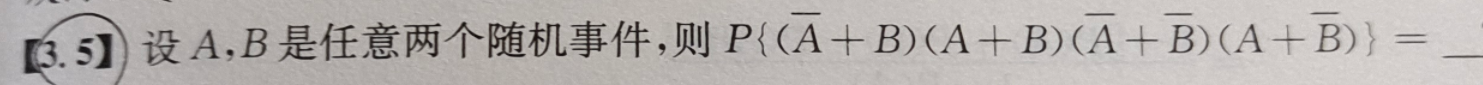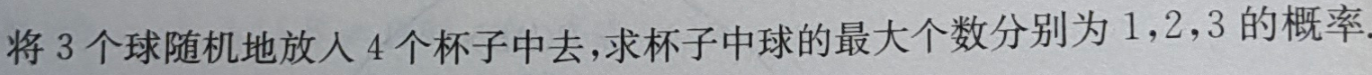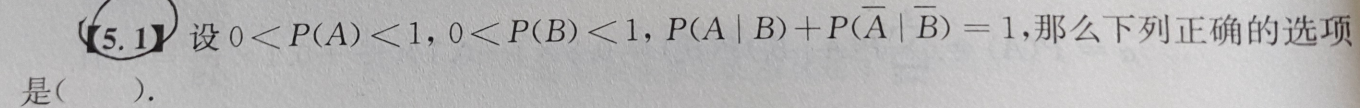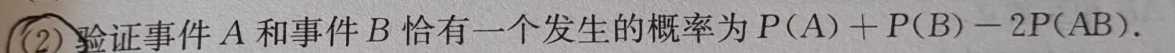第一章:随机事件及其概率
随机事件及其运算
事件的表示
Q:事件A,B,C中至少有两个发生,表示为
A:
AB∪BC∪AC
把两个发生的情况列出来,“至少”的话就是他们的组合啦
判断事件的关系及运算

法一:排除法,显然
法二:
A∪B=(A∪B)∪AB=(A∪B)∪(A∩B)
=(A∪B)∪(A∪B)=Ω

∵P(AB)=P(A)P(B∣A)≤P(A)
同理,P(AB)≤P(B)
∴2P(AB)≤P(A)+P(B)
∴C正确
随机事件的概率
古典概型

样本空间含有的样本数为34,该事件意味着:
- 前三次共摸到2种颜色的球,第四个球也随之固定:C32
- 这两种颜色的球,一种颜色2个,另一种颜色1个:C21
- 前三个球有顺序:C31
所以,概率为34C32C21C31=92
概率基本运算法则
利用性质求概率

由题意知,AB⊂C∴P(C)≥P(AB)
又∵P(A+B)=P(A)+P(B)−P(AB)
∴P(AB)=P(A)+P(B)−P(A+B)
∴P(C)≥P(A)+P(B)−P(A+B)≥P(A)+P(B)−1
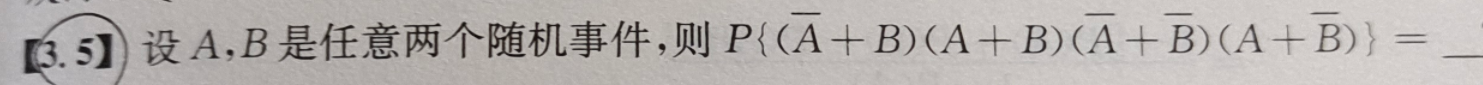
(A+B)(A+B)(A+B)(A+B)
=(A+B)(A+B)(A+B)(A+B)
=(AB+AB)(AB+AB)=∅
∴原式=0
利用公式求概率

设A={数字以0结尾},B={数字以5结尾},C={该数字被5整除},样本总数n为9×9×8×7,
|A|=9×8×7,∣B∣=8×8×7.
∴P(C)=n∣A∣+∣B∣
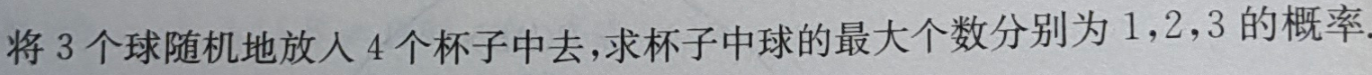
样本总数n为43,这是一次次放球推演出的样本总数,是有次序的,此时认为球是不同的,
设Bi={杯子中球的最大个数为i},
∣B1∣=C41A33,4个杯子选一个空着,3个球全排列;
∣B2∣=C41C31C32,4个杯子选一个放2个球,3个球选2个放进去,剩下3个杯子选一个放最后一个球;
∣B3∣=C41,4个杯子选一个放3个球。
∴P(Bi)=n∣Bi∣.

设A={至少有2只配成一双},则A={任意2只都不能配成一双},
从对立事件考虑,那么首先这4只必然来自4双鞋:C54,
然后,这4只鞋每一只都有“左或右”两种可能:24,
∴P(A)=1−P(A)=1−C104C5424=2113.
概率的综合应用

这题可以把n看作已知量,然后问当时选出的是正品的可能性,那就是典型的贝叶斯公式了,这题拐了个小弯,我第一次做的时候有点懵
设A={选出的是正品},B={使用n次未发生故障},
全概率公式:P(B)=P(A)P(B∣A)+P(A)P(B∣A)=0.1×1+0.9×(0.9)n,
贝叶斯公式:P(A∣B)=P(A)P(B∣A)+P(A)P(B∣A)P(A)P(B∣A)=0.1×1+0.9×(0.9)n0.1×1≥0.7,
∴n≥29.

没啥好说的,就典型的贝叶斯,可能需要注意的是随机选取(三分之一)和选的时候是有顺序的

也没啥好说的,就是注意一下约束条件,例如:只有甲炮射中的概率为0.4×(1−0.5)×(1−0.7),而不是0.4,容易忽略。
独立性
独立性判断
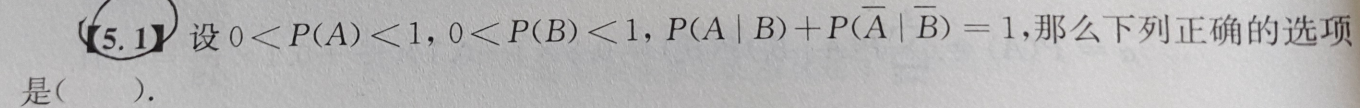

P(A∣B)+P(A∣B)=P(B)P(AB)+P(B)P(AB)
=P(B)P(AB)+1−P(B)1−P(A+B)
=P(B)P(AB)+1−P(B)1−P(A)−P(B)+P(AB)
=P(B)P(AB)+1+1−P(B)P(AB)−P(A)=1
∴P(B)P(AB)=1−P(B)P(A)−P(AB)
∴P(AB)−P(B)P(AB)=P(A)P(B)−P(B)P(AB)
∴P(AB)=P(A)P(B)
关于独立性与独立重复实验的问题

这里用到一个重要(冷门)公式,经常忘
P(AB)=P(B)−P(AB)
1.必要性
∵A,B相互独立∴A也与B相互独立,
∴P(B∣A)=P(B),P(B∣A)=P(B)∴P(B∣A)=P(B∣A).
2.充分性
∵P(B∣A)=P(B∣A)∴P(A)P(AB)=P(A)P(AB)=1−P(A)P(B)−P(AB),
∴P(A)P(B)−P(A)P(AB)=P(AB)−P(A)P(AB),
∴P(AB)=P(A)P(B).
∴A,B相互独立.

设A={甲获胜},A={乙获胜},Bi={甲第i轮射中},Ci={乙第i轮射中},
A=B1+B1C1B2+B1C1B2C2B3+...,
∴P(A)=p1+(1−p1)(1−p2)p1+(1−p1)2(1−p2)2p1+...,
=1−(1−p1)(1−p2)p1=p1+p2−p1p2p1,
∴P(A)=1−P(A).
证明题
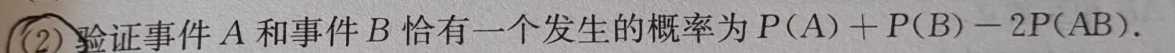
P(AB+AB)=P(AB)+P(AB)−0
=P(A)−P(AB)+P(B)−P(AB)=P(A)+P(B)−2P(AB)