古典概型
有放回抽样(二项分布)
P=(a+b)nCnkan−kbk=Cnk(a+ba)n−k(a+bb)k
不放回抽样(超几何分布)
P=Ca+bnCan−kCbk
生日问题
盒子模型
(我编的):把n个不同的球以相同的概率1/N随机放入N个(N≥n)盒 子中,且每个盒子能容纳的球数没有限制。
(1)事件A: 某指定的n个盒子各有一个球;
(2)事件B: 任何n个盒子各有一个球;
(3)事件C: 指定的某个盒子中恰好放入k个球(k<=n)

生日问题
求参加聚会的n(<=365)个人至少有两个人生日相同的 概率pn .
若把n个人看作上面的n个球,把一年中的365天作为盒子,则N=365, 所求的概率就是1 − P(B),
pn=1−p没有生日相同=1−365nA365n
抽签问题
一袋中有a个白球,b个黄球,记a+b=n.设每次 摸到各球的概率相等,每次从袋中摸一球,不放回地摸n次。 求第k次摸到白球的概率。
我们可以把抽签的过程,看作是n个球排成一排,被依次拿出的过程。那么,抽签的结果有a个白球的位置决定。
先从n个位置选出a个位置用来放白球,这是样本总体。
由于第k次摸到了白球,第k次摸到白球的情况数就是在n-1个位置选a-1个位置放剩余的白球。
P(Ak)=CnaCn−1a−1=na
几何概型
等车
汽车站每隔15分钟有一辆汽车到站,乘客到达车站 的时刻是随机的,求乘客候车时间不超过5分钟的概率. 在这个随机试验中,样本空间Ω = (0,15),且每个样本点 是等可能的 . {乘客候车不超过 5 分 钟 }这个事件是区间 (10,15)
P=1/3
约会
甲 、 乙两人相约在0到T这段时间内 ,在预定地点会面 . 先到的人等候另一个人 , 经过时间 t(t < T )后离去 .设每人在0到T这段时间内 各时刻到达该地是等可能的, 两人到达的时刻互不影响 . 求甲、乙两人能会面的概率 .
设 x , y 分别为甲、乙两人到达的时刻 , 则 0 ≤ x ≤ T , 0 ≤ y ≤ T. 两人会面的充要条件为|x −y| ≤ t ,
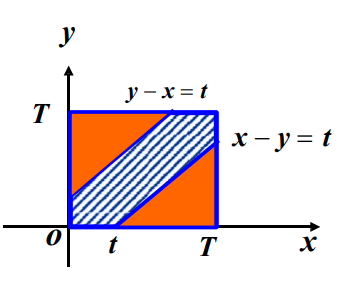
p=正方形面积阴影部分面积=T2T2−(T−t)2
蒲丰投针
平面上画有一组间距为a的平行线, 将一根长为l (0 < l < a)的针任意投掷在这个平面上,假设针落 在任意位置的可能性相同,试求针与平行线相交的概率.
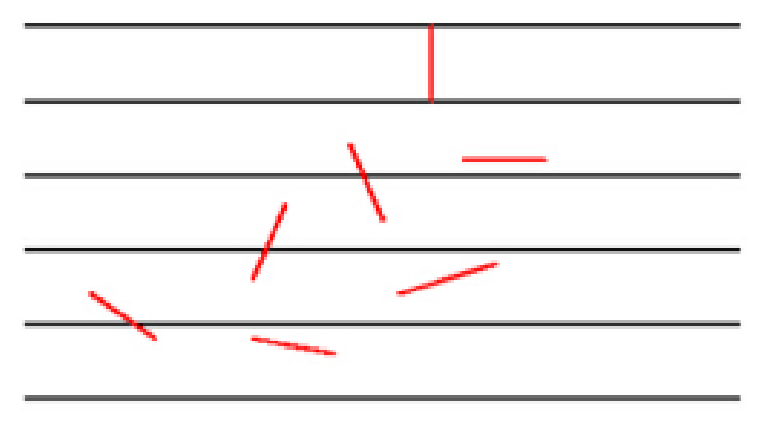
以x表示针的中点M到最近的一条平行直线的距离.ϕ表示针与该平行 直线的夹角. 那么针落在平面上的位置可由(x,ϕ)完全确定。
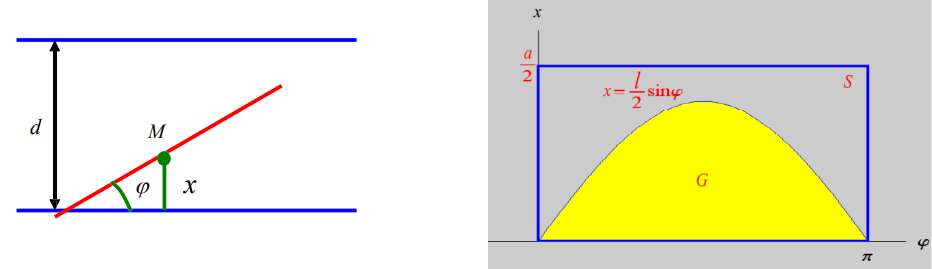
投针试验的所有可能结果对应矩形区域中的所有点
Ω={(x,ϕ)∣0≤x≤2a,0≤ϕ≤π}
所关心的事件A = {针与某一平行直线相交} 发生的充分必要条 件为Ω中的点满足
0\leq x\leq\frac l 2 \sin \phi,0\leq\phi\leq\pi\
P(A)=∣Ω∣∣G∣=2aπ∫02π2lsinϕdϕ=πa2l
因此,可以用此方法估计圆周率
蒙特卡罗方法
设计一个随机试验,用一个事件的概率来估计我们感兴趣 的一个量,在计算机上模拟所设计的随机试验,这样的方法称 为蒙特卡罗方法(Monte Carlo method)或随机模拟法。
蒙特卡罗(Monte Carlo)算法计算圆周率
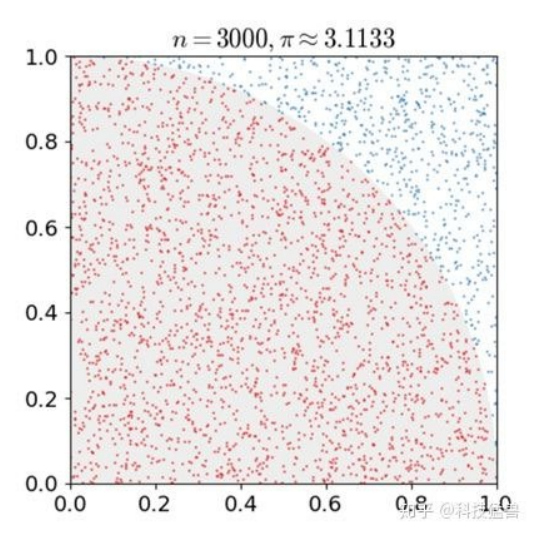
给定边长为1的正方形,画其内切圆,然后在正方形内随机打点,设点落在圆内的概 为P,则根据几何概型,
P = 圆面积 / 正方形面积 = PI * (1/2) * (1/2) / 1 = PI / 4
本质上,和蒲丰投针是一样的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include <iostream>
#include <ctime>
using namespace std;
int main()
{
const int MAX_TIMES = 20000000;
srand(static_cast<unsigned int>(time(0)));
for (int j = 0; j < 10; j++) {
int in = 0;
for (int i = 0; i < MAX_TIMES; i++){
double x = static_cast<double>(rand()) / RAND_MAX;
double y = static_cast<double>(rand()) / RAND_MAX;
if (x * x + y * y <= 1.0){
in++;
}
if (i % (MAX_TIMES / 100) == 0) { cout << "."; }
}
double pi = 4.0 * in / MAX_TIMES;
cout << "\nPI=" << pi << endl;
}
return 0;
}
|
主观概率
主观概率是指对事件发生的可能性的定量描述,是指建立在过去的经 验与判断的基础上确定的概率,反映的只是一种主观可能性。
(1)有的试验自然状态无法重复;如明天是否下雨;手术是否 成功;明年国民经济增长率如何;能否考上研究生;
(2)试验费用过于昂贵、代价过大;如洲际导弹命中率。
概率的公理化定义
设随机试验E的样本空间为Ω,若对E 的每一事件A,都有一个实数P(A)与之对应,并且满足下 列三条公理(Axioms),则称P(A)为事件A的概率。
(1)非负性(Non-negativity) 对每一个事件A,有 P(A) ≥ 0
(2)规范性(Unitarity) P(Ω) =1
(3)可列可加性(Countable Addition rule) 对任意可数个两两互不相容事件A1, A2 ,…, 有 P(∑Ai) = ∑P(Ai).
概率的性质

加法公式
P(i=1⋃nAi)=1≤i≤n∑P(Ai)−1≤i<j≤n∑P(AiAj)
+1≤i<j<k≤n∑P(AiAjAk)−⋯+(−1)n−1P(i=1⋂nAi)
特例:
P(AՍB)=P(A)+P(B)-P(AB)
P(AՍBՍC)=P(A)+P(B)+P©-P(AB)-P(AC)-P(BC)+P(ABC)
概率连续性

概率不等式
如果A⊆B,则P(A)≤P(B)
max(P(A),P(B))≤P(A∪B)≤min(P(A)+P(B),1)
minP(A),P(B)≥P(A∩B)≥max(P(A)+P(B)−1,0)
P(A∪B)=P(A)+P(B)−P(A∩B)≤P(A)+P(B)
AB⊆A∪B,且P(A)P(B)≤P(A∪B)







