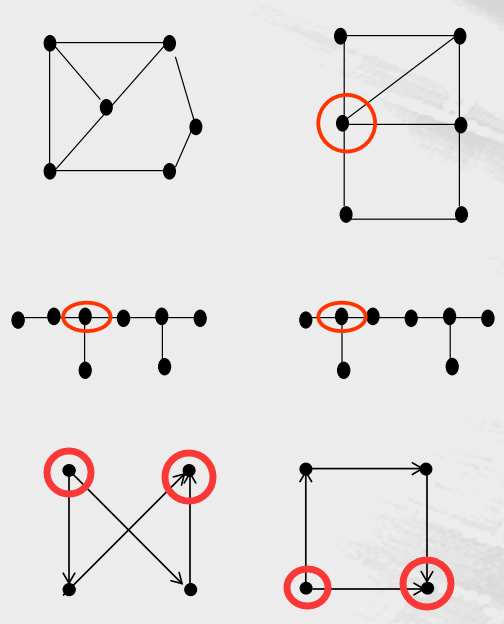
离散数学02
简单图
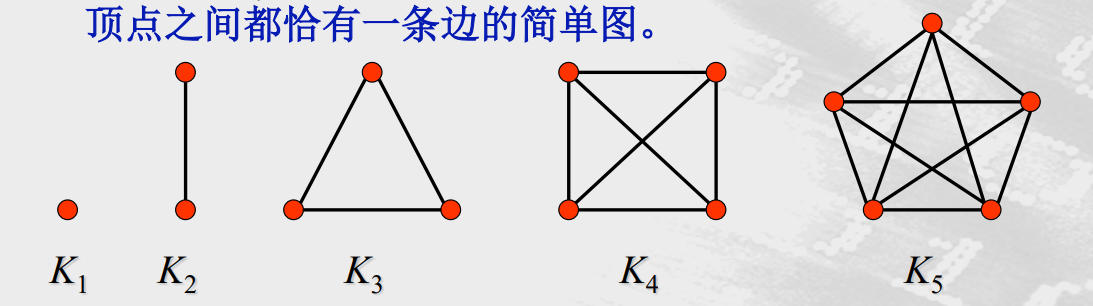
完全图
n个顶点的完全图是在任意每对不同顶点之间都恰有一条边的简单图。
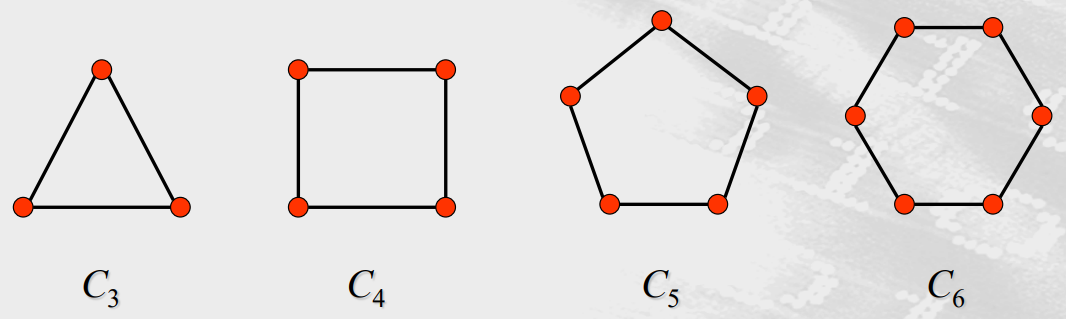
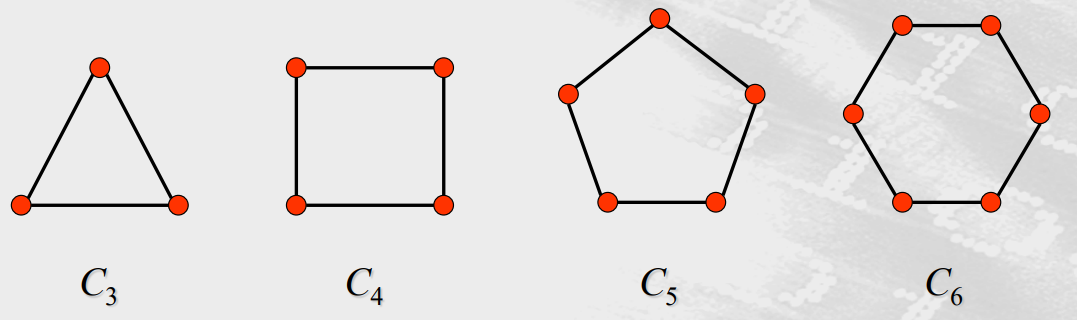
圈图(n>2)
轮图(n>2)
当给圈图 添加另一个顶点,而且把这个顶点与圈图里n个顶点逐个连接时,就得出轮图。
n立方体图
n立方体图是用顶点表示 个长度为n的位串的图。两个顶点相邻,当且仅当他们所表示的位串恰恰相差一位。
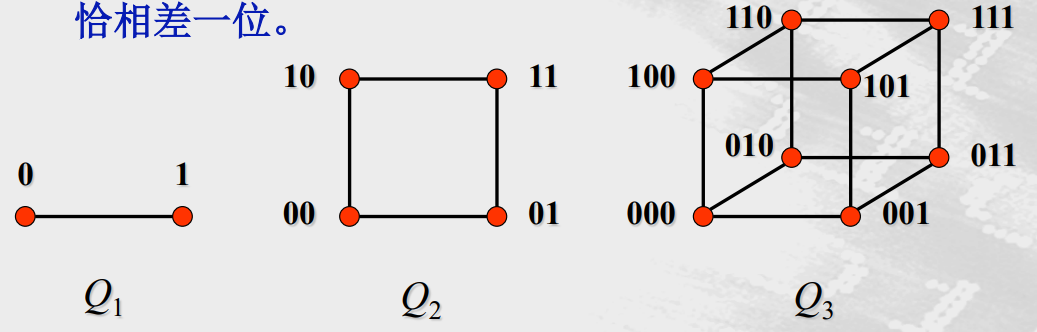
偶图(二分图)
若把简单图G的顶点集分成 两个不相交的非空集合V1和V2,使得图里的每一条边都连接着V1 里的一个顶点与V2里的一个顶点,则G称为偶图
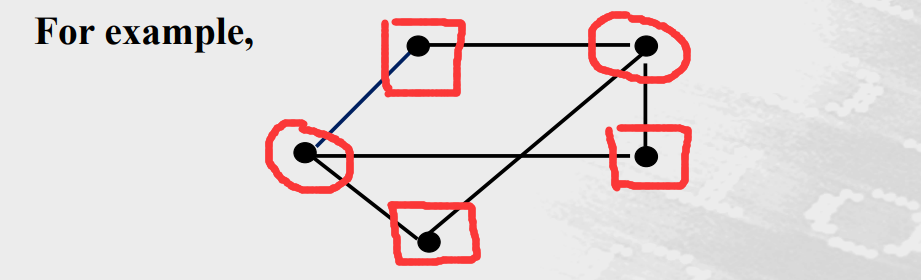
找法:从一个点开始找,一直扩散到全图。
完全偶图
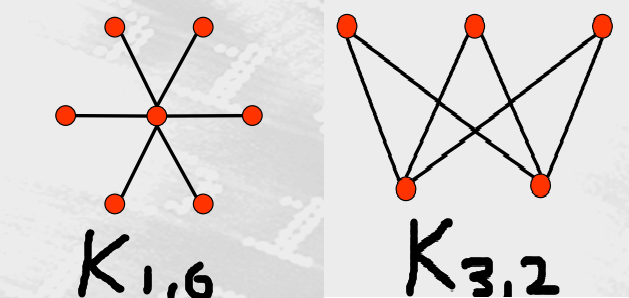
完全偶图是顶点集分成分别含有 m和n个顶点的两个子集的图。两个顶点之间有边当且仅 当一个顶点属于第一个子集而另一个顶点属于第二个子集。
正则图(regular)
每个顶点有相同的度,如果度都为n,则称为n-regular
推论:
-
是一个(n-1)-regular
-
当m=n时,是正则图
生成图
定义:就那样
求一个图的生成子图的个数(公式是我写的,错就错啦)
边导出子图
设G是一个图,E1⊆E(G),以E1为边集,E1中边的端点全体为顶点集构成的子图,称为由E1 导出的G的子图(边导出子图),记为G(E1)。
点导出子图
又设V1⊆V(G),以V1为顶点集,端点均在V1中的边的全体为边集,构成的子图,称为由V1导出的G的 子图(点导出子图),记为G(V1)。
注意事项
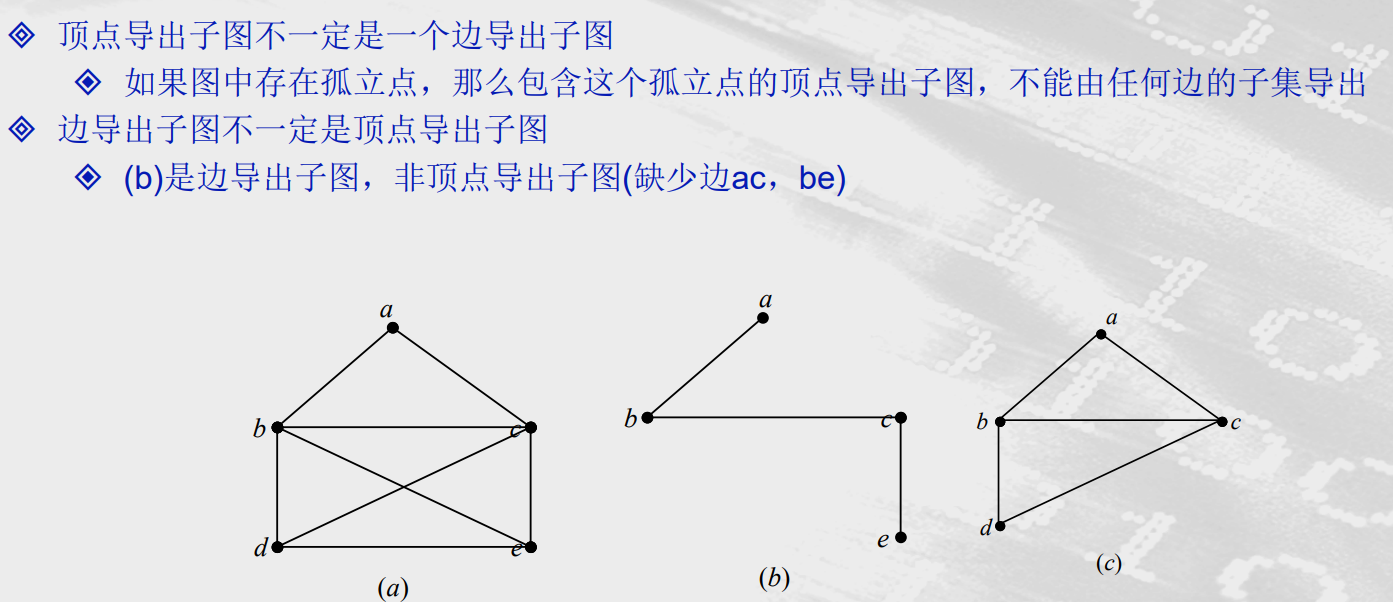
补图
设G是具有n个顶点的简单图,从这n个顶点构成的完全图中删去G的所有边,但保留顶点 集V(G)所得到的图称为G的补图,简称G的补,记为~G。
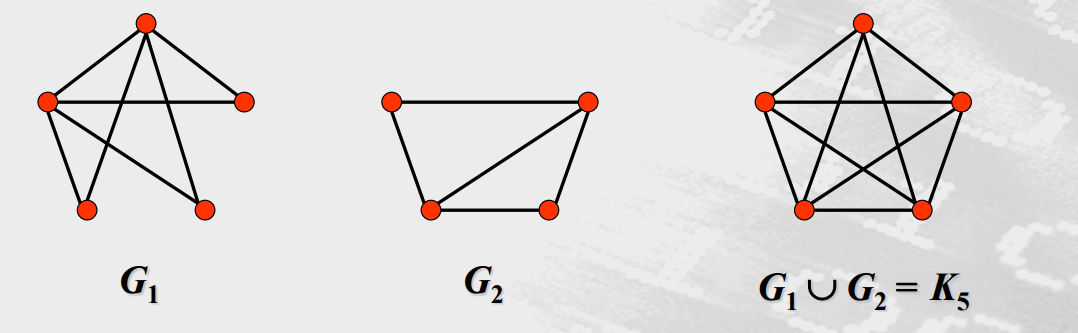
图的并(union)
设
图的表示
邻接表
狗都不用

邻接矩阵
- 简单无向图:关于主对角线对称,只有0/1,主对角线为0
- 无向多重图:数字为边的数量
- 无向伪图:主对角线上有1,主对角线上应该没有除0/1之外的数
- 有向图:是否有边(0/1),不对称
对无向图来说,邻接矩阵每一 行各个位置上数字之和代表该顶点的度减去自环数(0/1)
对于有向图而言,邻接矩阵每一行各个位置上 数字之和代表该顶点的出度
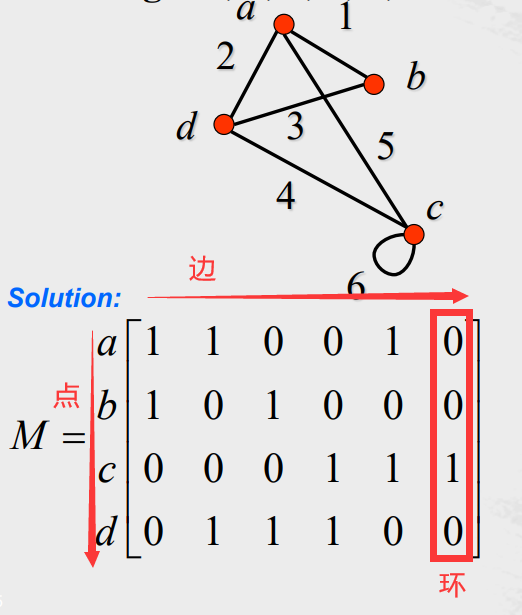
关联矩阵
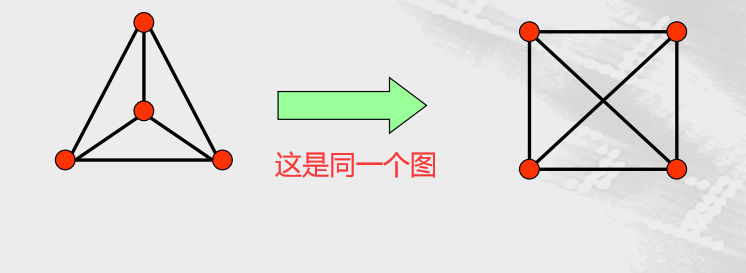
图的同构
定义
设$ 和$$G_2= (V_2, E_2)$是简单图,若存在一对 一的和映上的从 V1 到V2 的函数f,且f具有这样的性质, 对V1里所有的a 和 b来说,a和b在 G1里邻接,当且仅当 f(a)和 f(b)在 G2里邻接,就说G1和G2是同构的。这样的 函数 f 称为同构.
换句话说,当两个简单图同构时,两个图的顶点之间 具有保持邻接关系的一一对应。
判断是否同构
在两个带n个顶点的简单图顶点集之间有n!种可能的一一对应(第一个顶点有n种对应方式,第二个有n-1种……),通过检验每一种对应来看它是否保持邻接关系和不邻接关系是不可行的。
但是,我们有办法排除不同构的情况。需要依赖不变量。
同构图中的重要不变量
所谓的“不变量”不仅指某些数字量相同,更本质的说是指“顶点之间的邻接特征”不变,需要活用。
- 相同的顶点数、边数、顶点度数(找两个图的最大度数顶点,有向图要区分入度和出度)
- 如果一个是二分图/完全图/轮图/立方体……,那么另一个也是二分图/完全图/轮图/立方体……
- 一个点与其对应点不仅度数相同,而且其相邻点的度数也一一对应相同
结论
1.直觉观察
2.看是否违反上述不变量
例: