离散数学01

图的概述

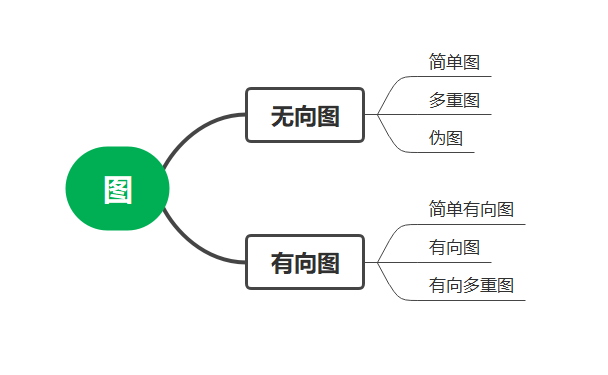
无向图

A simple graph G=(V,E) consists of vertices, V, and edges, E, connecting distinct elements of V.

简单图G=(V,E)是 由非空顶点集V和边集E所组成的，V的不同元素的无序对称为边。

• no loops 没环
• can‘t have multiple edges joining vertices 两个顶点间最多只 有一条边

A multigraph allows multiple edges for two vertices.

多重图允许顶点对之间有多重边

A pseudograph is a multigraph which permits loops.

伪图也是多重图，它可以存在环

有向图

简单有向图

由非空顶点集V、边集E所组成的，边V中 元素的有序对。不允许有环，不允许在两个顶点之间有同向的多重边。

有向图 有时也写作D = (V, A)

In a directed graph G = (V, E) the edges are ordered pairs （有序对）of (not necessarily distinct) vertices.

有向图(V,E)是由非空顶点集V、边集E所组成的，边V中 元素的有序对。允许有环(即相同元素的有序对)，但不允许在两个 顶点之间有同向的多重边。

有向多重图

In a directed multigraph G = (V, E) the edges are ordered pairs of (not necessarily distinct) vertices, and in addition there may be multiple edges.

有向多重图 G=(V,E)是由非空顶点集V、边集E组成的,其中可以存在多重边。

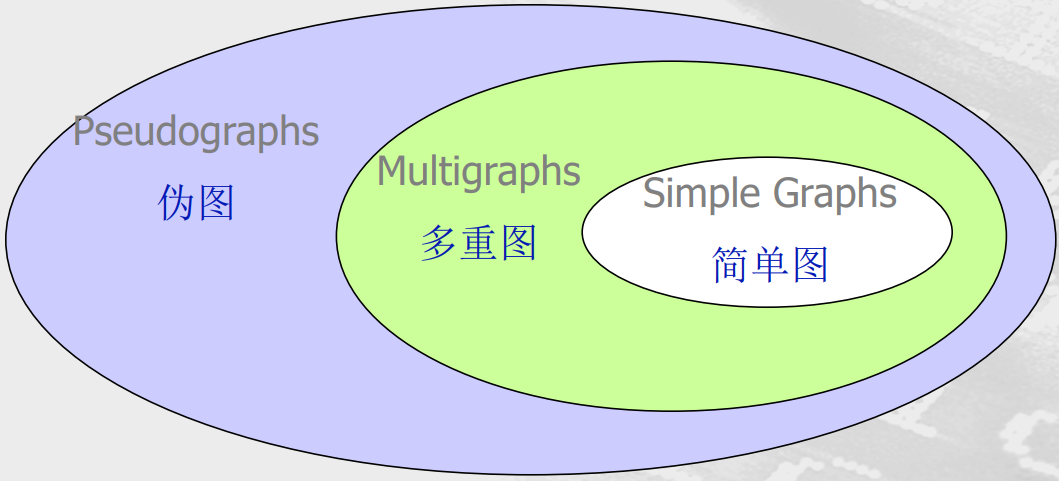
总结

类型	边	多重边？	环？
简单图 simple graph	无向	N	N
多重图 Multigraph	无向	Y	N
伪图 Pseudograph	无向	Y	Y
简单有向图	有向	N	N
有向图 directed graph	有向	N	Y
有向多重图 dir. Multigraph	有向	Y	Y

图的术语

基本术语

顶点（vertex)、边 (edge)、邻接或相邻 (adjacent or neighbors)、连接 (incident with)、端点 (endpoints)、环 (loop)

度 (degree)

顶点的度是与该顶点关联的边的数目，例外的情形是，顶点上的环为顶点的度做出双倍贡献。

If deg(v) = 0, v is called isolated.孤立的

If deg(v) = 1, v is called pendant.悬挂的

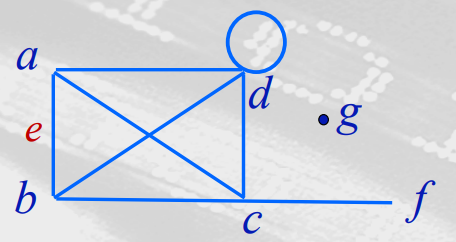
如下，abcdgf点的度分别为3，3，4，5，0，1；g点是孤立的，f点是悬挂的。

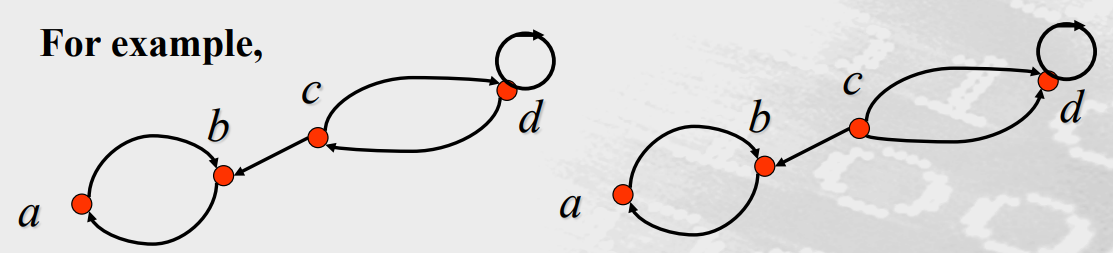
入度（The in degree） 顶点v的入度是以 v作为终点的边数。表示为

$$deg^-(v)$$

出度（the out degree ）顶点v的出度是 以v作为起点的边数。表示为

$$deg^+(v)$$

定理

1、握手定理（The Handshaking Theorem）

设G=(V,E)是e条边的无向图，则

$$\sum_{v\in V}deg(v)=2e$$

其实对有向图也成立，不知道为什么要指明无向图

2、无向图有偶数个奇数度顶点

设V1和V2分别 是偶数度顶点和奇数度顶点的集合

$$\sum_{v\in V_1}deg(v)+\sum_{v\in V_2}deg(v)=2m$$

3、入度和 = 出度和 = 边数

$$\sum_{v\in V}deg^-(v)=\sum_{v\in V}deg^+(v)=|E|$$