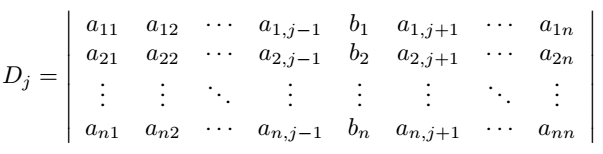大一下线性代数期末复习

1.行列式解方程组

1.1克莱默法则

用来解线性方程组

$$Ax=b\\\\ 写成(a_1,a_2,\cdots,a_n)x=b,\quad a_n为列向量$$

设A的行列式为D，

若D = 0，则方程组无解或有无数组解

若D不为0，则线性方程组有唯一解，其解为

$$x_j=\frac{D_j}{D},\quad j=1,2,\cdots,n \\ \\ 其中D_j=(a_1,a_2,\cdots,a_j-1,b,a_j+1,\cdots,a_n)$$

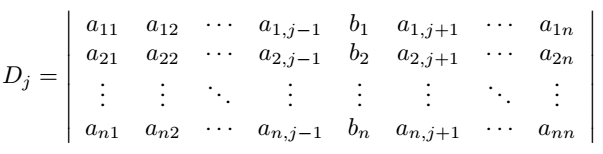
1.2线性方程组的解

行空间与与零空间互补

从行列式的角度来说，如果行列式不为零，那么有唯一解；如果行列式等于零，有可能无解，也有可能有无数组解。

例如：

其行列式的值为

$$\lambda^2(\lambda+3)\newline\newline 当\lambda=0时，有无穷多解\newline 当\lambda=-3时，无解$$

2.逆矩阵的求法

2.1定义法

利用待定系数的方法求解，例如：

$$有矩阵A = \begin{bmatrix}1&2\newline\newline-1&-3 \end{bmatrix},\quad 设它的逆为A^{-1}=\begin{bmatrix}a&b\newline c&d \end{bmatrix}\newline\newline 那么，根据定义AA^{-1}=I,\quad解方程组即可$$

二阶矩阵要解4个方程，三阶矩阵要解9个方程，四阶矩阵要解16个方程……

可以看出此方法的局限性，也就解个二阶矩阵用用

2.2伴随矩阵法

伴随矩阵是由原矩阵各项的代数余子式组成的

代数余子式：

$$A= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\newline a_{21}&a_{22}&\cdots&a_{2n}\newline \vdots&\vdots&\ddots&\vdots\newline a_{n1}&a_{n2}&\cdots&a_{nn} \end{bmatrix}\newline\newline a_{ij}的代数余子式为\quad(-1)^{i+j} \left|\begin{matrix} a_{11}&a_{12}&\cdots&a_{1,j-1}&a_{1,j+1}&\cdots&a_{1n}\newline a_{21}&a_{22}&\cdots&a_{2,j-1}&a_{2,j+1}&\cdots&a_{2n}\newline \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots\newline a_{i-1,1}&a_{i-1,2}&\cdots&a_{i-1,j-1}&a_{i-1,j+1}&\cdots&a_{i-1,n}\newline a_{i-1,1}&a_{i-1,2}&\cdots&a_{i-1,j-1}&a_{i-1,j+1}&\cdots&a_{i-1,n}\newline \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots\newline a_{n1}&a_{n2}&\cdots&a_{n,j-1}&a_{n,j+1}&\cdots&a_{nn} \end{matrix}\right|\newline\newline 例如a_{22}的代数余子式为\quad(-1)^{2+2} \left|\begin{matrix} a_{11}&a_{13}&\cdots&a_{1n}\newline a_{31}&a_{33}&\cdots&a_{3n}\newline \vdots&\vdots&\ddots&\vdots\newline a_{n1}&a_{n3}&\cdots&a_{nn} \end{matrix}\right|$$

伴随矩阵:

把每一项都求代数余子式，再把所得的值替换掉原来的项就得到了新矩阵，把这个新矩阵再转置，就得到了伴随矩阵A*。

求逆：

$$A^{-1}=\frac{A^*}{|A|}$$

不可不谓之暴算，等我大汗淋漓求出此逆之时，早就收卷了

2.3初等变换法

把要求逆的矩阵的右边拼上一个单位阵，进行初等行变换，使得单位阵变到左边，剩下右边的为原矩阵的逆。

$$A= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\newline a_{21}&a_{22}&\cdots&a_{2n}\newline \vdots&\vdots&\ddots&\vdots\newline a_{n1}&a_{n2}&\cdots&a_{nn} \end{bmatrix}\newline\newline 取A_1=[A,I_n]\newline A_1= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}&1&0&\cdots&0\newline a_{21}&a_{22}&\cdots&a_{2n}&0&1&\cdots&0\newline \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\newline a_{n1}&a_{n2}&\cdots&a_{nn}&0&0&\cdots&1 \end{bmatrix}$$

然后，通过行化简，化为：

$$A_2=[I_n,A^{-1}]\newline\newline A_2= \begin{bmatrix} 1&0&\cdots&0&a'_{11}&a'_{12}&\cdots&a'_{1n}\newline 0&1&\cdots&0&a_{21}&a'_{22}&\cdots&a'_{2n}\newline \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\newline 0&0&\cdots&1&a'_{n1}&a'_{n2}&\cdots&a'_{nn} \end{bmatrix}\newline\newline 右侧的部分就是A的逆A^{-1}$$

爱了，爱了

3.分块矩阵

3.1加法与数乘与乘法

与普通矩阵的运算法则一致

3.2转置

类比分步求导，先以各分块为单位作转置，再把各分块内部取转置。

例：

$$A = \begin{bmatrix} A_{11}&A_{12}\newline A_{21}&A_{22} \end{bmatrix}\newline\newline A^T= \begin{bmatrix} A_{11}^T&A_{21}^T\newline A_{12}^T&A_{22}^T \end{bmatrix}$$

3.3分块上三角矩阵的逆

$$A = \begin{bmatrix} A_{11}&A_{12}\newline O&A_{22} \end{bmatrix}\newline\newline A^T= \begin{bmatrix} A_{11}^{-1}&-A_{11}^{-1}A_{12}A_{22}^{-1}\newline O&A_{22}^{-1} \end{bmatrix}$$

软工大一学的到此为止，上网一查直接吓坏了

分块矩阵行列式

分块矩阵求逆

还有秩……

4.向量线性相关和线性无关

4.1基的变换

设B\{b_1,b_2,\cdots,b_n\}和C\{c_1,c_2,\cdots,c_n\}都是向量空间V的基，则存在一个n\times n的矩阵\underset{C\leftarrow B}{P}使得\newline\newline [x]_C =\underset{C\leftarrow B}{P} [x]_B\newline\newline 其中，变换矩阵\underset{C\leftarrow B}{P} 的列向量是基B中的向量对应在C坐标下的向量，即\newline\newline \underset{C\leftarrow B}{P}=[\quad[b_1]_C\quad[b_2]_C\quad\cdots\quad[b_3]_C\quad]\newline\newline 因为\underset{C\leftarrow B}{P}是可逆的，所以(\underset{C\leftarrow B}{P})^{-1}= \underset{B\leftarrow C}{P}

为了实现两个非标准基之间的变换，我们需要原来的基关于新的基的坐标变换。

什么？我是谜语人？看例子

例一：已知变换矩阵求基

$$对于一个向量空间V，考虑两个基B\{b_1,b_2\},C\{c_1,c_2\},满足\newline b_1=4c_1+c_2,\quad b_2=-6c_1+c_2\newline\newline 已知[x]_B= \begin{bmatrix} 3\newline1 \end{bmatrix} ,求[x]_C\newline\newline 解：因为[x]_B= \begin{bmatrix} 3\newline1 \end{bmatrix}，\quad 所以x = 3b_1+b_2\newline 所以，[x]_C=[3b_1+b_2]_C\newline =3[b_1]_C+[b_2]_C\newline =[[b_1]_C\quad[b_2]_C] \begin{bmatrix} 3\newline1 \end{bmatrix}\newline\newline 又因为，b_1=4c_1+c_2,\quad b_2=-6c_1+c_2\newline 所以，[b_1]_C= \begin{bmatrix} 4\newline1 \end{bmatrix}, [b_2]_C= \begin{bmatrix} -6\newline1 \end{bmatrix}\newline\newline 所以，[x]_C= \begin{bmatrix} 4&-6\newline1&1 \end{bmatrix} \begin{bmatrix} 3\newline1 \end{bmatrix}= \begin{bmatrix} 6\newline4 \end{bmatrix}$$

例二：已知基求变换矩阵

$$对于一个向量空间V，考虑两个基B\{b_1,b_2\},C\{c_1,c_2\}，\newline 已知b_1= \begin{bmatrix} -9\newline1 \end{bmatrix}, b_2= \begin{bmatrix} -5\newline-1 \end{bmatrix}, c_1= \begin{bmatrix} 1\newline-4 \end{bmatrix}, c_2= \begin{bmatrix} 3\newline-5 \end{bmatrix}, 求变换矩阵\underset{C\leftarrow B}{P}\newline\newline 写出系数矩阵[c_1\quad c_2\quad b_1\quad b_2]= \begin{bmatrix} 1&3&-9&-5\newline -4&-5&1&-1 \end{bmatrix}\newline 行化简得 \begin{bmatrix} 1&0&6&4\newline 0&1&-5&-3 \end{bmatrix}\newline 所以\underset{C\leftarrow B}{P}= \begin{bmatrix} 6&4\newline -5&-3 \end{bmatrix}$$

4.2施密特正交化

4.2.1.定义

施密特正交化（Schmidt orthogonalization）是求欧氏空间正交基的一种方法。从欧氏空间任意线性无关的向量组α1，α2，……，αm出发，求得正交向量组β1，β2，……，βm，使由α1，α2，……，αm与向量组β1，β2，……，βm等价，再将正交向量组中每个向量经过单位化，就得到一个标准正交向量组，这种方法称为施密特正交化。

4.2.2.计算

以此矩阵为例

$$\begin{matrix} 1&0&0\newline 1&1&0\newline 1&1&1\newline 1&1&1\newline \end{matrix}$$

将矩阵写为无关向量组的形式，一般取列向量组a1，a2，……，am

$$a_1 = \begin{bmatrix}1\newline 1\newline 1\newline 1 \end{bmatrix}, a_2 = \begin{bmatrix}0\newline 1\newline 1\newline 1 \end{bmatrix}, a_3 = \begin{bmatrix}0\newline 0\newline 1\newline 1 \end{bmatrix}$$

正交化：

$$b_1=a_1\newline b_2 = a_2-\frac{<a_2,b_1>}{<b_1,b_1>}b_1\newline b_3 = a_3 - \frac{<a_3,b_1>}{<b_1,b_1>}b_1 - \frac{<a_3,b_2>}{<b_2,b_2>}b_2\newline ...\newline b_n = a_n - \frac{<a_n,b_1>}{<b_1,b_1>}b_1 - \frac{<a_n,b_2>}{<b_2,b_2>}b_2 - ...-\frac{<a_n,b_{n-1}>}{<b_{n-1},b_{n-1}>}b_{n-1}\newline$$

注：

$$<a,b>表示向量内积，即点乘$$

例中：

$$b_1= a_1 = \begin{bmatrix}1\newline 1\newline 1\newline 1 \end{bmatrix}\newline b_2 = a_2-\frac{<a_2,b_1>}{<b_1,b_1>}b_1 =a_1-\frac{3}{4}b_1=\begin{bmatrix}-3\newline 1\newline 1\newline 1 \end{bmatrix}\newline b_3 = a_3 - \frac{<a_3,b_1>}{<b_1,b_1>}b_1 - \frac{<a_3,b_2>}{<b_2,b_2>}b_2=a_3-\frac{1}{2}b_1-\frac{1}{6}b_2=\begin{bmatrix}0\newline -2\newline 1\newline 1 \end{bmatrix}\newline$$

单位化：

$$\varepsilon_n = \frac{b_n}{||b_n||},\newline 标准正交基为\{\varepsilon_1,\varepsilon_2,...,\varepsilon_n\}$$

例中：

$$\varepsilon_1 = \frac{b_1}{||b_1||}=\begin{bmatrix}\frac{1}{2}\newline \frac{1}{2}\newline \frac{1}{2}\newline \frac{1}{2} \end{bmatrix},\newline \varepsilon_2 = \frac{b_2}{||b_2||} = \begin{bmatrix}-\frac{\sqrt{3}}{2}\newline \frac{\sqrt{3}}{6}\newline \frac{\sqrt{3}}{6}\newline \frac{\sqrt{3}}{6} \end{bmatrix},\newline \varepsilon_3 = \frac{b_3}{||b_1||} = \begin{bmatrix}0\newline -\frac{\sqrt{6}}{3}\newline \frac{\sqrt{6}}{6}\newline \frac{\sqrt{6}}{6} \end{bmatrix}\newline$$

4.2.3.不唯一

正交化的向量组不唯一. 按施密特正交化过程, 我们将向量组中的向量打乱顺序得到的向量组也不一样，标准正交基也不是唯一的.

5.等价、相似、合同

矩阵等价

$$若存在可逆阵P和Q，使得B=PAQ，则称矩阵A与B等价，记作A\cong B$$

充要条件：A和B的秩相等

矩阵合同

$$若存在可逆阵P，使得B=P^TAP，则称矩阵A与B合同，记作A\underset{-}{\sim} B$$

矩阵相似

$$若存在可逆阵P，使得B=P^{-1}AP，则称矩阵A与B相似，记作A\sim B$$

三者关系：

$$A\underset{-}{\sim} B\Rightarrow A\cong B\newline \newline A\sim B\Rightarrow A\cong B\newline 反之，均不成立$$

一般而言，相似与合同没有关系。但是，正交相似与正交合同是同一回事。而且实对称矩阵一定与对角阵合同。

7.特征值特征向量

定义：

$$A是n阶方阵，\lambda是一个数字，若存在非零向量\alpha，使得A\alpha=\lambda\alpha, 则称\lambda为特征值，非零向量\alpha为矩阵A对应与特征值\lambda的特征向量。$$

求法：

$$满足|A-\lambda E|=O的数\lambda为特征值\newline \newline 方程组(A-\lambda E)X=O的非零解或基础解系为特征向量$$

例：

$$求矩阵A= \begin{bmatrix} 1&-2&2\newline -2&-2&4\newline 2&4&-2\newline \end{bmatrix}的特征值，特征向量\newline \newline \left|\begin{matrix} 1-\lambda&-2&2\newline -2&-2-\lambda&4\newline 2&4&-2-\lambda\newline \end{matrix}\right|\newline \newline =\cdots=-\lambda^3-3\lambda^2+24\lambda-28\newline \newline 猜根，根往往是常数项的因子，\newline \newline 解得，上式=-(\lambda-2)^2(\lambda+7)\newline \newline \lambda_1=\lambda_2=2，\lambda_3=-7\newline \newline ①对于\lambda_1=\lambda_2=2，\newline A-2E= \begin{bmatrix} -1&-2&2\newline -2&-4&4\newline 2&4&-4\newline \end{bmatrix}\sim \begin{bmatrix} -1&-2&2\newline 0&0&0\newline 0&0&0\newline \end{bmatrix}\newline \newline \Rightarrow x_1=-2x_2+2x_3\newline \newline 所以，\xi_1=\begin{bmatrix}-2\newline 1\newline 0 \end{bmatrix}， \xi_1=\begin{bmatrix}2\newline 0\newline 1 \end{bmatrix}\newline \newline 特征值为2的全部特征向量为k_1\xi_1+k_2\xi_2\newline \newline ②同理可得，\lambda=-7的特征向量\xi_3=\begin{bmatrix}1\newline 2\newline -2 \end{bmatrix}\newline \newline 其全部特征向量为k_3\xi_3\newline \newline k_1,k_2,k_3均不为0$$

性质：

$$若\lambda是A的特征值，那么：\newline \newline 1.A^T的特征值是\lambda\newline 2.A^{-1}的特征值是\lambda^{-1}\newline 3.kA的特征值是k\lambda\newline 4.A^m的特征值是\lambda^m\newline 5.f(A)的特征值是f(\lambda)\newline 6.A^*的特征值是\frac{|A|}\lambda\newline 7.\lambda_1\lambda_2\cdots \lambda_n=|A|\newline 8.\lambda_1+\lambda_2+\cdots +\lambda_n=a_{11}+a_{22}+\cdots+a_{nn}$$

8.二次型

化二次型为标准型

(1)把二次型系数写成实对称矩阵

(2)施密特正交单位化

(3)组成变换矩阵，得对角阵，即得标准型

分类

正定、负定，不定

特征值为正，则是正定阵

特征值为负，则是负定阵

特征值既有正的也有负的，则是不定阵

9.QR分解

看这